发布日期:2025-5-9 11:15:17
1、引言
损伤容限评估方法已成为航空发动机寿命限制件的设计与服役管理的核心内容,其中转子部件裂纹扩展寿命的准确预测是损伤容限评估的关键环节[1-3]。与标准紧凑拉伸(CT)试样中的穿透型初始裂纹不同,转子寿命限制件的初始裂纹往往萌生于机械加工导致的表面缺陷或者冶金过程引入的内部缺陷,具有一定的三维形貌特征。对于发动机轮盘中的典型半圆形埋入表面裂纹,从裂纹前缘与轮盘表面的交点到裂纹前缘最深点,应力状态由近平面应力状态逐渐转变为近平面应变状态,而这种裂纹前缘不同位置应力状态的不同,会引起裂纹尖端微小区域约束效应(又称拘束度)的不同,进而导致裂纹扩展有效驱动力不同[4-7]。在分析表面疲劳裂纹扩展问题时,考虑裂纹前缘不同位置的三维约束效应可以建立更为准确的裂纹扩展模型,进而评估转子寿命限制件的损伤容限性能,支撑发动机安全设计与服役管理。
求解裂尖约束效应的基础是建立能够准确描述裂尖应力应变场分布的方法。基于线弹性条件下的裂尖区域应力强度因子K场或弹塑性条件下裂尖HRR(Hutchinson-RiceRosengreen)解,学者们提出了包括K-T、J-Q、K-T-Tz、J-T、J-A2、J-Q-Tz等双参数、三参数描述方法[8-12]。Williams等[13]首先建立了裂尖应力场K-T双参数描述,使用非奇异T应力提高K的描述精度,并反映面内约束,O'Dowd等使用Q参数来反映弹塑性条件下裂纹面内的约束效应[14]。在描述面内约束的T、Q参数基础上,郭万林[15]引入了离面约束因子Tz表征面外约束效应,以更全面反映三维裂纹体尖端的应力状态。于培师等[16-17]分析了不同构件的角裂纹、表面裂纹等三维裂纹前缘不同位置处的Tz分布,并提出将裂纹前缘的Tz分布等效为不同厚度板内中心穿透裂纹前缘的Tz分布。赵军华等[18]基于Tz提出考虑面外约束的K-Tz双参数理论。为了结合面内约束和面外约束的影响,郭万林等[19]进一步提出了K-T-Tz、J-Q-Tz等三参数理论描述裂纹前缘三维应力场,并通过对比K-T、J-Q分析结果,指出三参数理论能更准确地解释三维应力场。
鉴于三参数方法对裂尖应力场描述的复杂性,一种思路是构建一个综合性参数作为约束效应的表征参数,Mostafavi等[20]使用当前裂尖塑性区的面积与高约束作用下裂尖塑性区面积比值φ来表征裂尖约束效应,该参数不适用于大范围屈服情况。杨杰等[21]提出了一个基于裂尖等效塑性应变面积的统一约束因子,综合反映裂尖面内和面外的约束效应。考虑到塑性应变面积计算的复杂性,徐建勇等[22]进一步使用裂尖张开位移比值作为综合约束因子。然而上述研究多用于裂纹体的断裂韧性研究,针对不同约束作用下的裂纹扩展研究,Newman[23]首先在条带屈服模型基础上引入裂尖约束因子,将其定义为最大主应力与屈服应力之比,指出金属材料平面应力和平面应变状态下的约束因子分别为1和3。Machniewicz等[24]指出,裂纹张开时裂尖前方塑性区内不同位置的约束因子呈抛物线型分布。Newman等[25]通过数学处理给出了裂尖前方平均约束因子,指出其会随裂纹加载情况、裂纹体厚度和裂尖塑性区大小发生变化。Daniewicz[4]使用应力强度因子切片合成方法近似计算三维表面裂纹的裂纹面位移和裂尖塑性区尺寸。郭万林等[26]、Wang等[27]和McMaster等[28]分别给出了约束因子的经验公式。吴连生等[29]、许磊[30]、周斌[31]利用约束因子预测了不同厚度穿透裂纹和表面裂纹的裂纹扩展速率。这些模型或者求解复杂或者需要基于试验数据拟合,如何快速、准确计算不同载荷和厚度下的裂尖三维约束因子,成为裂纹扩展预测的关键因素之一。
随着有限元技术的不断发展,结合数据分析程序进行联合仿真,为三维裂纹前缘不同位置处拉伸塑性区和变约束因子的计算提供了有力手段。本文将采用Newman提出的约束因子描述裂纹前缘约束程度,以TC4钛合金表面裂纹小尺寸试样为研究对象,构建裂纹前缘不同位置约束因子快速计算方法,获得约束因子随外加载荷、裂纹尺寸以及裂纹形状的变化规律,并与传统的计算模型进行对比。
2、分析方法
2.1表面裂纹试样有限元模型
本文所研究材料为直接从发动机风扇盘中心孔区域取样的TC4钛合金。为确保该材料的各项同性特征,为后续三维约束因子计算提供支撑,从周向(CD)、径向(RD)和轴向(AD)三个方向分别取样,并进行金相分析、硬度测试和拉伸试验。图1给出了TC4合金的三维显微组织,各方向上均呈现出典型等轴组织特征,平均晶粒尺寸分别为21.6μm、21.8μm和23.1μm,基本一致。三个方向维氏硬度测量结果分别为316HV、324HV和321HV,呈现出与组织一样的均匀性特征[32]。
图2为TC4钛合金三个方向的拉伸曲线,三个方向拉伸性能差异较小,结合组织和硬度测试结果,表明本研究所用TC4钛合金材料具有各向同性特征,为后续表面裂纹三维弹塑性应力场分析和约束因子计算提供了支撑。采用弹塑性Ramberg-Osgood模型描述拉伸曲线:
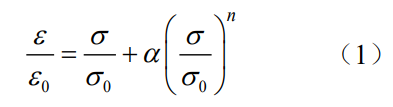
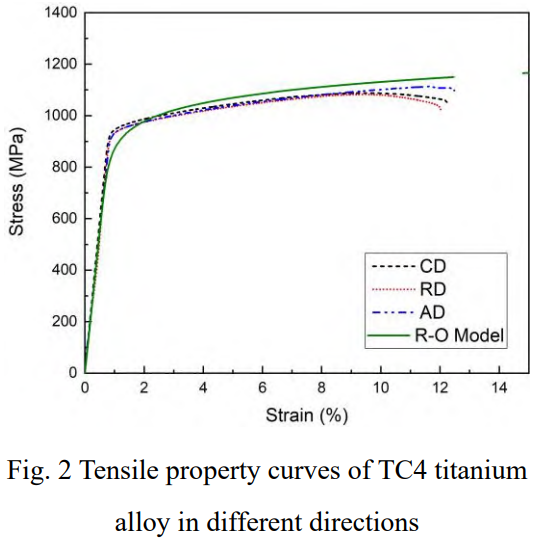
式中,ε0=σ0/E,屈服强度σ0=960MPa,弹性模量E=110GPa,参数α=0.227,n=14.33。
参考文献[33]中表面裂纹(surfacecrack,SC)试样尺寸并考虑疲劳试验机实际夹持要求,设计图3所示SC试样,其中夹持段为Φ12.7mm圆棒,标距段为43.38mm2的矩形截面。在标距段中间位置置入表面裂纹如图3(b)所示,其中半轴长分别为a和c,试样厚度为t,远端外加应力为S。考虑到试样对称性,选取试样中段的1/4部分进行有限元建模,并保证加载面和边界条件不影响表面裂纹周围应力场。
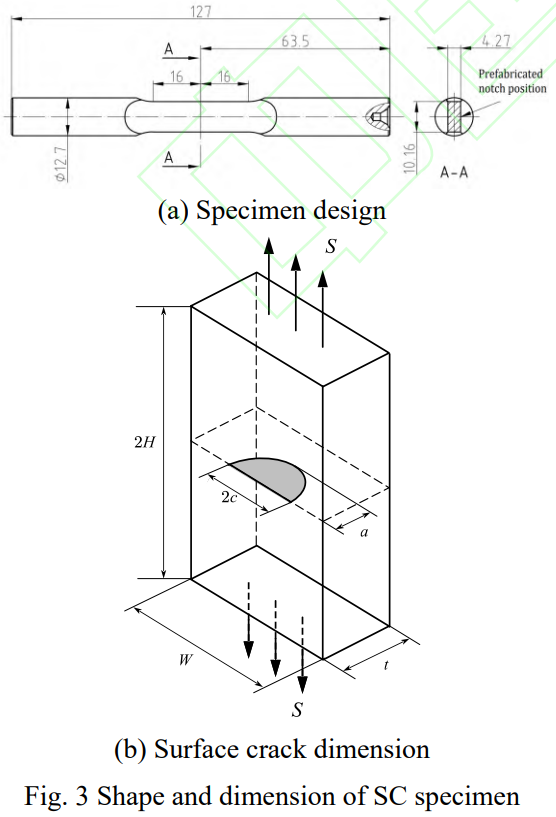
保持试样尺寸不变,设定不同的裂纹深度比a/t、裂纹半轴比a/c以及加载应力S/σ0,以研究不同裂纹尺寸、形状以及外加载荷水平下的约束效应,具体取值如下:a/t=0.05,0.1,0.2,0.4,0.6;a/c=0.75,0.9,1,1.1,1.25,1.4,1.55;S/σ0=0.45,0.5,0.54,0.59。对上述参数进行组合计算,累积共5×7×4=140个算例。
2.2自适应程序化网格生成方法
考虑到算例较多,建立自适应程序化表面裂纹试样单元设置和网格划分流程,实现不同算例网格模型的快速构建,具体步骤为:
(1)求解表面裂纹应力强度因子Kmax。利用公式(2)估算表面裂纹在表面点和最深点处裂纹面内的塑性区尺寸rp,其中表面点和最深点处的约束因子α分别取为1和3。
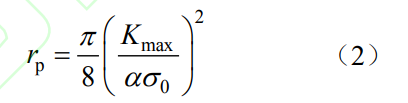
(2)将裂纹前缘线周围空间分割为管状区域以便于网格划分。将该管状区域分为内管状域crackt,i和外管状域crackt,o,对应的半径分别为Rt,i和Rt,o。对Rt,i和Rt,o进行赋值使得裂纹前缘最小塑性区尺寸rp,min≥Rt,i且最大塑性区尺寸rp,max≤Rt,o。
(3)在管状域外围划分过渡域crackb作为网格过渡区域。设定该过渡域的截面尺寸为Lb,r≈2Rt,o,Lbox,s≈2Rt,o。
(4)按上述方法和尺寸要求,对含表面裂纹的几何模型进行分割,分割后的实体均可划分六面体网格。含表面裂纹几何模型的分割方式、局部关键尺寸如图4(a)所示。
(5)设定裂纹前缘节点数Nf和过渡域crackb外侧节点数Nb,c。为了保证过渡域中网格从裂纹前缘一侧到无裂纹一侧能够顺利过渡,一般设定Nb,c=Nf/3。
(6)设定内管状域crackt,i和外管状域crackt,o的截面径向节点数目Nt,i和Nt,o,以及周向节点数目Nθ,以保证塑性区有足够的网格数。同时为了确定合适的网格尺寸以保证计算结果的准确性,对裂尖前方不同网格密度的有限元模型进行多次试算发现,当裂尖前方塑性区内网格数目在10个以上时,最终计算的约束因子数值变化在1%以内,该结果与Daniewicz等[34]研究一致。本文设定周向节点数Nθ=16,确保塑性区内至少包含10个单元。
(7)利用管状域截面径向和周向结点进行管状域截面的网格划分,然后通过扫掠方式沿裂纹前缘曲线实现裂纹前缘方向管状域的整体网格划分。截面网格与裂纹前缘曲线垂直,保证每个裂纹前缘位置处截面网格均为围绕裂纹尖端的同心环形分布。
(8)设定过渡域crackb的截面节点数分别为Nb,r≈8,Nb,s≈4,合理设定其余实体的网格节点数以保证单元尺寸过渡平顺。
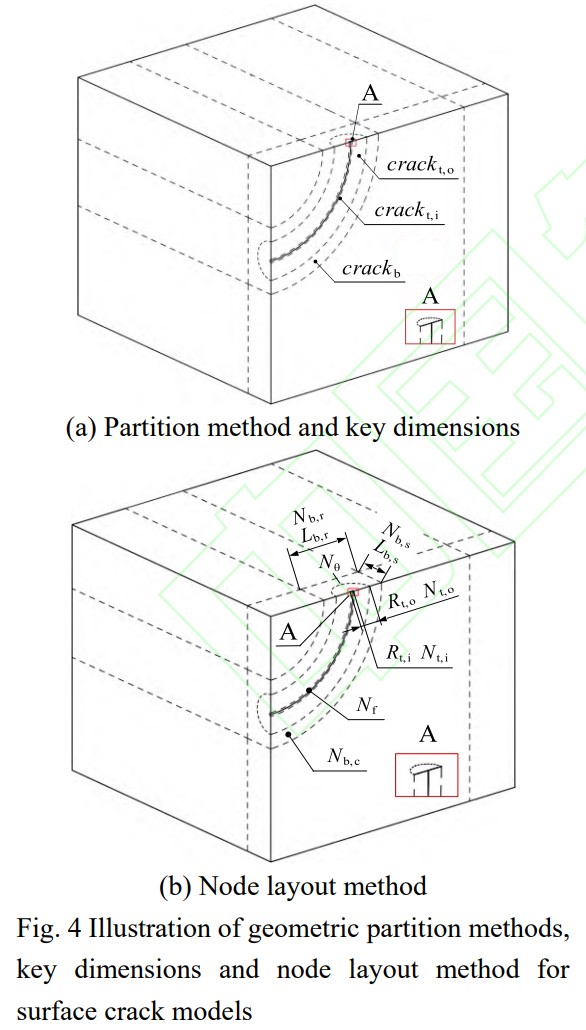
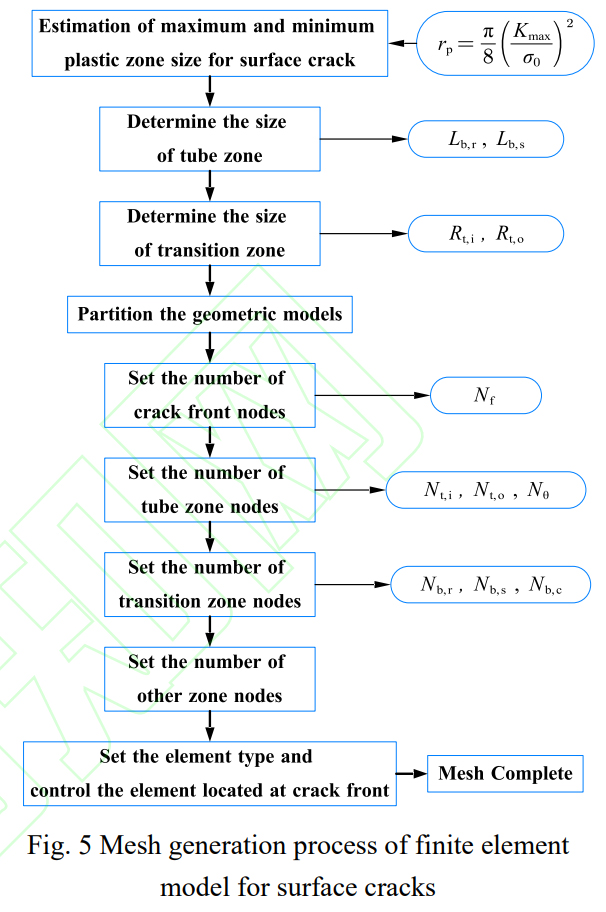
(9)使用六面体二次减缩积分单元对全部有限元实体进行网格划分,保证网格质量满足弹塑性分析要求。将与裂纹前缘相连的单元面坍缩为裂纹前缘上的线段,坍缩到同一位置的节点并不会缩并为一个节点,在后续加载过程中各节点仍可自由移动。这样处理能近似取得裂纹前缘接触单元内应变r-1的渐近趋势。图5给出了表面裂纹试样程序化网格划分流程。
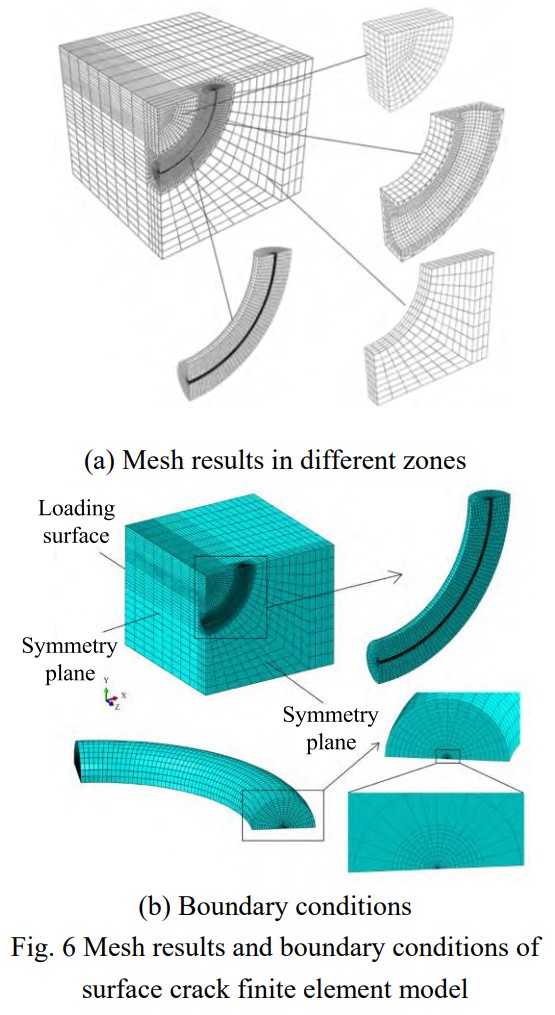
通过Abaquspythonscript前处理脚本对所有表面裂纹算例进行网格划分。图6(a)为表面裂纹不同区域网格划分情况,可见所有区域均可由六面体单元组成,网格由裂纹区的密集分布逐渐过渡到试样表面的相对稀疏状态。图6(b)给出了最终的网格模型和边界条件,在模型端面施加轴向拉伸载荷,在对称面施加对称边界条件。
2.3裂纹前缘三维约束因子计算
在Newman等基于条带屈服模型的约束效应研究中,约束因子α通常基于三维弹塑性有限元分析的裂尖塑性区内应力分布进行求解。对于表面裂纹前缘任意一点,将该点裂尖塑性区内不同位置处垂直于裂纹面的拉伸应力σyy与屈服强度σ0比值进行平均,即得到约束因子α:
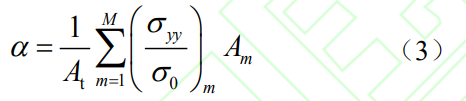
式中,m为裂纹前缘塑性区中单元编号,M为塑性区内单元总数目,(σyy/σ0)m是塑性区内裂纹面法向拉伸应力与屈服应力的比值,Am是单元m的面积,At是塑性区中所有单元的总面积。图7给出了约束因子α的计算示意图。
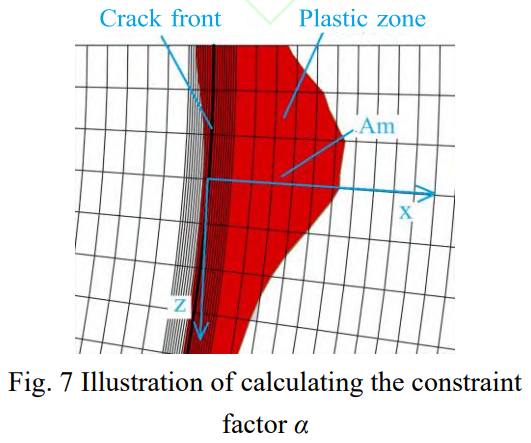
利用公式(3)对裂纹前缘不同位置的塑性区约束因子α进行计算。考虑到计算过程复杂且算例数量较大,通过编制Abaquspythonscript后处理脚本实现上述计算过程。裂纹前缘不同位置使用归一化弧度φ表示,φ从0到1表示裂纹前缘从一侧与试样表面交点位置到另一侧与试样表面交点位置,φ=0.5表示裂尖前缘位于试样内部最深位置。
3、结果与讨论
3.1表面裂纹前缘应力分布
图8(a)为典型载荷下表面裂纹前缘弹塑性有限元分析结果,图中灰白颜色区域表示裂尖塑性区,塑性区内至少包含10个单元,验证了程序化网格划分方法的有效性。裂尖塑性区呈现出试样表面位置尺寸大、内部位置尺寸小的特点。为进一步深入分析,提取裂纹前缘裂纹面上塑性区的边界,与裂纹前缘一同绘制,如图8(b)所示。从图中可见,裂纹面内裂尖塑性区尺寸在试样浅表层处达到最大,最外层表面处的塑性区尺寸略低于浅表层处尺寸;随着裂纹前缘深度的增加,裂纹面内塑性区尺寸迅速减少并逐渐稳定,在最深点处达到最小尺寸。
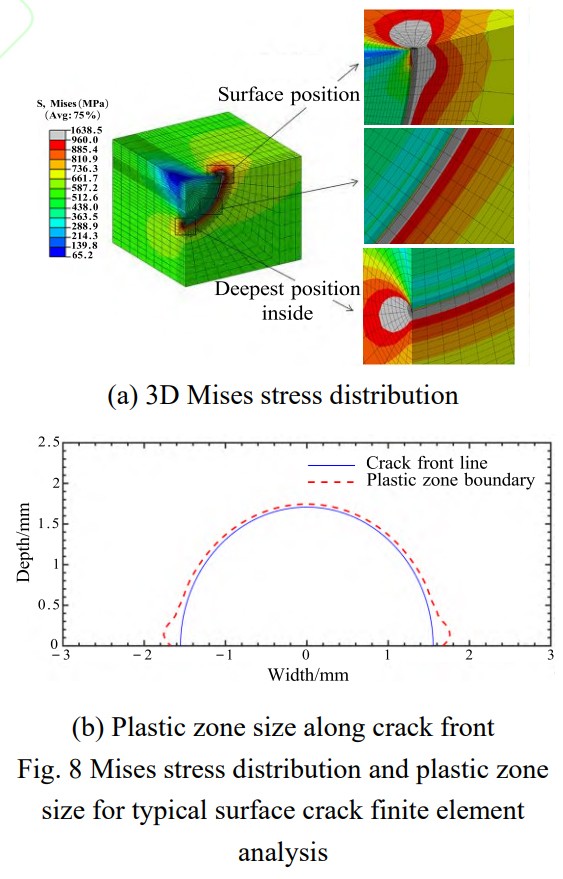
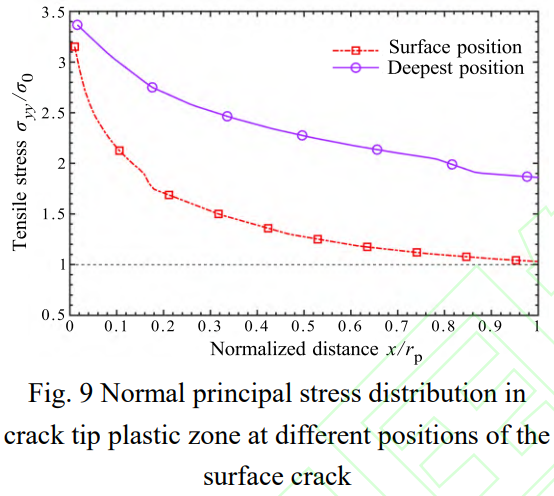
为了研究表面位置和内部最深处裂纹前缘裂尖应力场,提取相应位置塑性区内裂纹面拉伸应力σyy/σ0随到裂尖距离的分布曲线,如图9所示。为便于比较,到裂尖距离通过相应位置的塑性区尺寸rp进行归一化处理。图中可见,表面和内部最深处裂纹前缘裂纹面上的拉伸应力随到裂尖距离的增大均呈抛物线型分布,与Machniewicz等[24]研究结果一致。内部最深处裂尖塑性区内的拉伸应力整体均大于表面位置裂尖塑性区内拉伸应力且下降趋势更为缓慢,这是裂纹前缘不同位置约束作用不同导致的结果。
3.2表面裂纹前缘三维约束因子
图10给出了远场应力S/σ0=0.5情况下,4种裂纹形状(半轴比a/c=0.75,1.0,1.25,1.55),5种裂纹尺寸(裂纹厚度比a/t=0.05,0.1,0.2,0.4,0.6)表面裂纹前缘不同位置约束因子α分布情况。从图中可以看出,α随着裂纹前缘的位置变化近似呈“倒U型”,表面点处α数值在1.25左右,接近于平面应力状态。随着裂纹前缘位置远离试样表面,α迅速增大进而趋向稳定,最深处α数值在2.5左右,接近平面应变状态。相同裂纹形状a/c下,当裂纹相对尺寸a/t从0.05增大到0.4时,表面和最深处α变化相对较小,浅表层处则有较为明显的下降;当a/t继续增大到0.6时,裂纹前缘不同位置处α均出现明显下降。此时裂纹尺寸已大于试样截面厚度一半,试样整体约束作用显著减小,进而导致α整体下降。相同裂纹尺寸-试样厚度比a/t下,当半轴比a/c从0.75增大到1.55时,α整体变化不大,可见约束因子主要受表面裂纹深度方向最大尺寸影响。
图11为裂纹相对尺寸a/t=0.4时,不同应力水平下(S/σ0=0.45,0.5,0.54,0.59),4种裂纹形状(半轴比a/c=0.75,1.0,1.25,1.55)表面裂纹前缘不同位置约束因子分布情况。图中可知,固定裂纹尺寸和形状,随着外加应力水平的增大,表面点处α基本保持不变而最深点处的α有较为明显的下降。此外,半轴比a/c=1.55情况下α随载荷增大的下降幅度要小于半轴比a/c=0.75的情况。当裂纹相对尺寸a/t保持不变时,a/c越大表示裂纹表面长度越小;可见,裂纹尺寸较小时,α对载荷变化更不敏感。
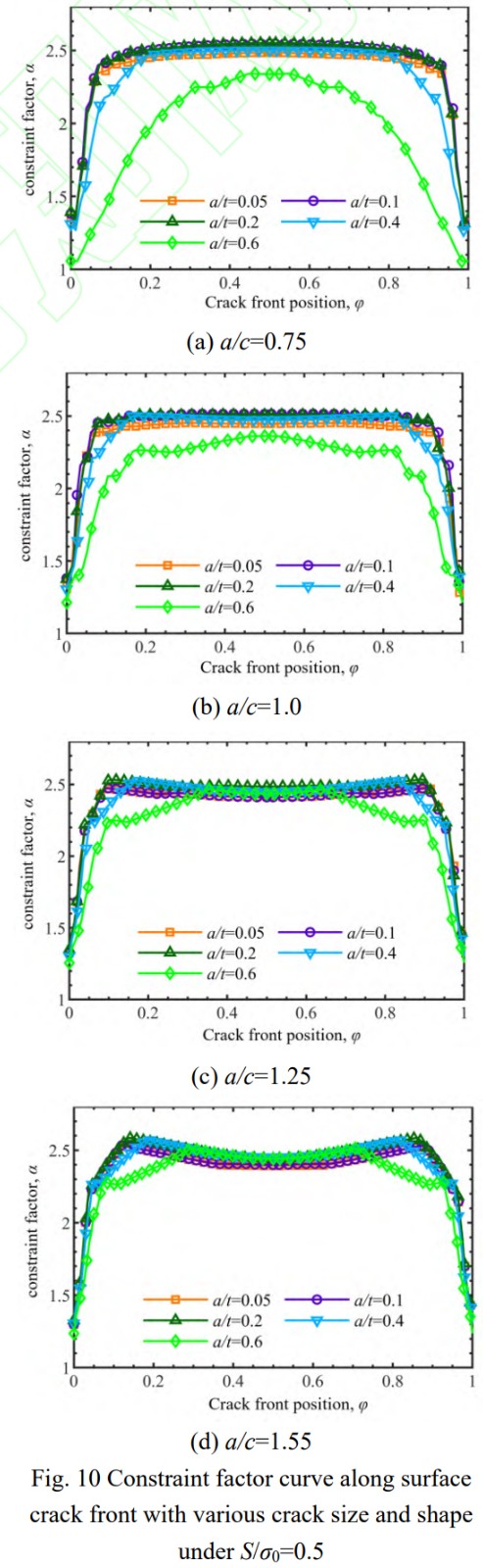
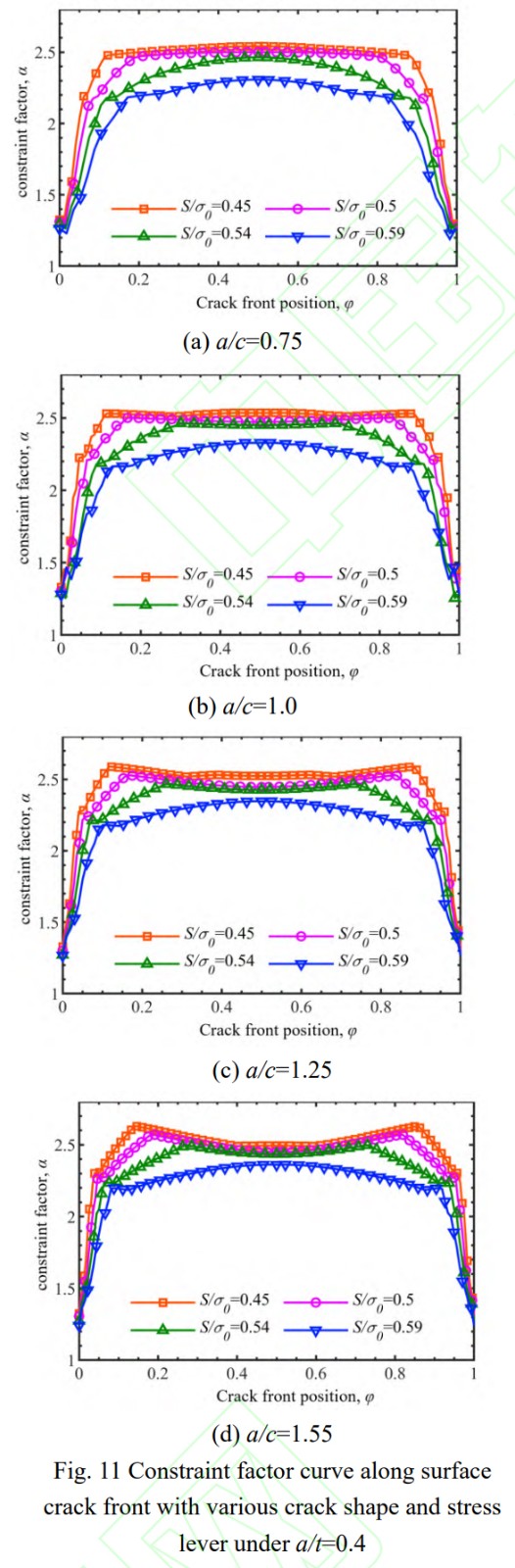
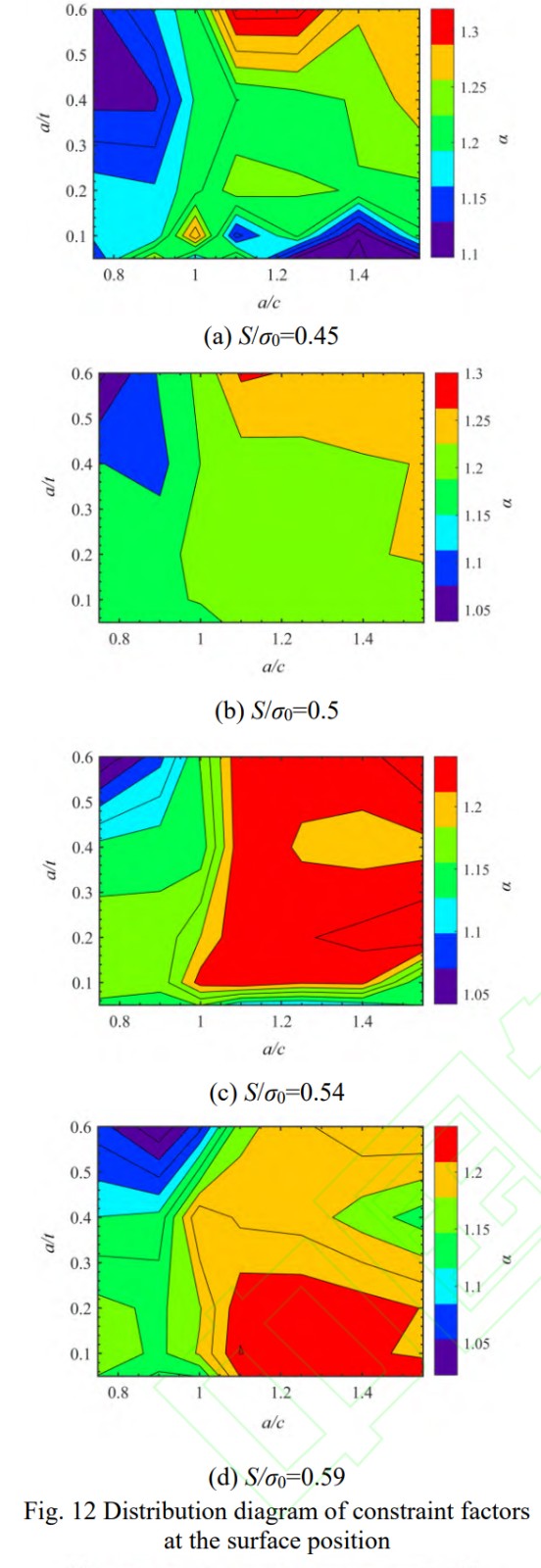
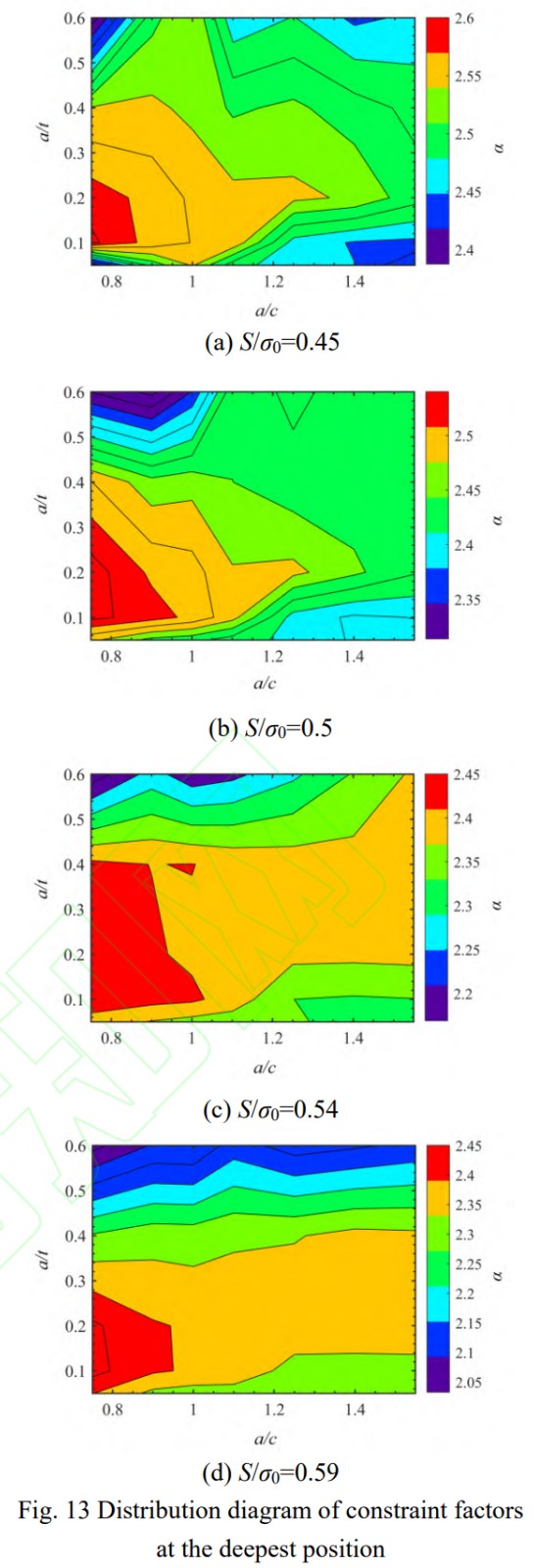
针对典型尺寸、形状和应力水平下的表面裂纹,分别提取表面位置和最深位置处的裂纹前缘α,绘制等值图如图12和图13所示。对比两图可以发现,最深点处α随裂纹尺寸和裂纹形状变化的分布规律在不同加载水平下基本一致,最大值均分布在a/t=0.15,a/c=0.8附近;而表面点处α随裂纹尺寸和裂纹形状变化的分布规律在不同加载水平下有明显差异:载荷水平较小时,α最大值出现在a/t=0.6,a/c=1.2附近;载荷水平较大时,α最大值出现在a/t=0.1,a/c=1.3附近。
3.3适用性分析
为分析本文提出的约束因子计算方法的适用性,与Guo方法进行对比研究。Guo等[26]将有限厚板穿透裂纹中约束因子α的数值解与归一化的平面应力裂尖塑性区尺寸rp0/t相联系,给出了约束因子计算公式:
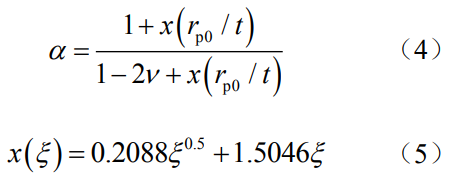
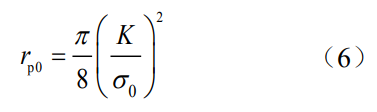
式中,rp0为加载时裂纹前缘裂纹面上塑性区尺寸,t为试样厚度,ν为材料泊松比。进一步地,于培师等[16-17]基于离面约束等效原则,通过表面裂纹前缘任一点处的离面约束参数Tz与厚度为Beq的中心穿透直裂纹厚度方向平均离面约束参数Tz相同的原则,将表面裂纹前缘上任一点处的约束状态等效为一定厚度的中心穿透裂纹约束状态。经过系统分析表面裂纹前缘不同位置处Tz的分布,得到裂纹前缘线上弧度为φ的位置处等效厚度的拟合公式:
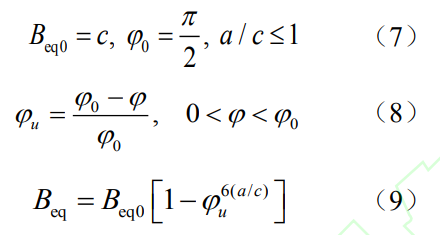
联合式(4)~式(9),可以求得表面裂纹前缘上不同位置处的约束因子α值。
图14给出了使用本文三维有限元分析方法得到的表面裂纹前缘最深点处约束因子与Guo方法计算的约束因子对比结果。
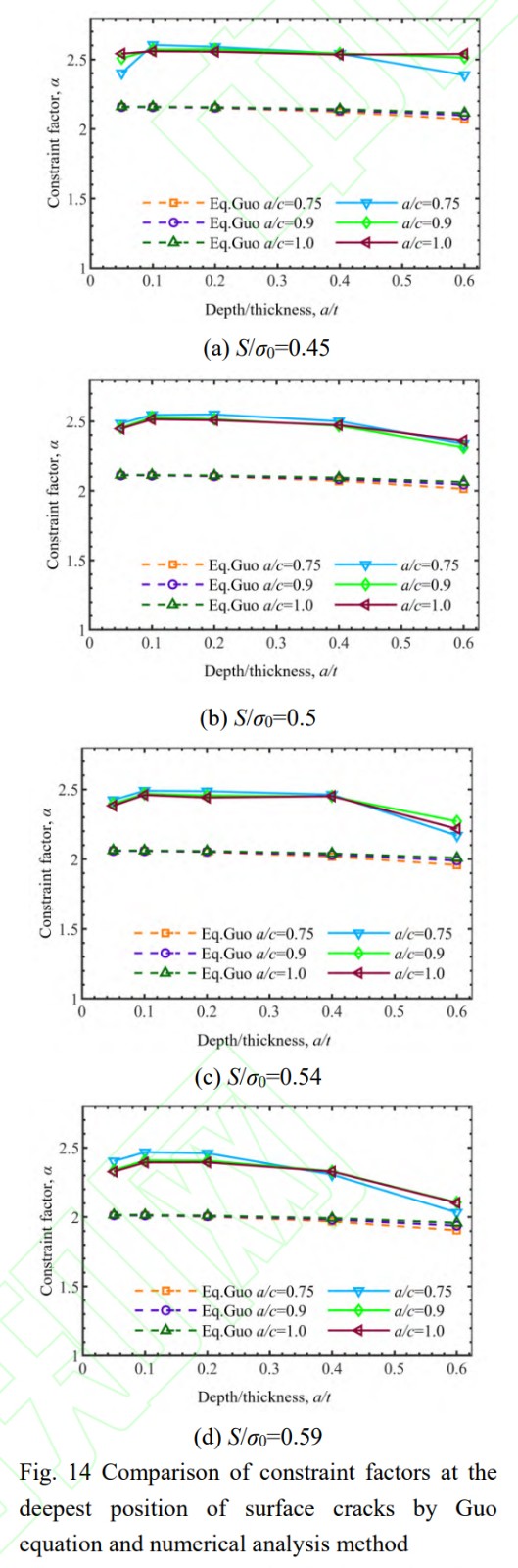
可以看到,Guo方法计算结果和本文有限元分析结果均能反映表面裂纹最深点处约束因子随着载荷水平以及裂纹尺寸的增加总体呈减小趋势。但Guo方法计算的约束因子值较本文有限元分析结果偏小,且随a/t和a/c的变化趋势不如本文有限元分析结果显著。这可能是由于Guo方法通过厚度等效以及数据拟合等手段获得了计算方程,存在一定的平均效果,而有限元数值仿真更能反映局部应力、裂纹形状以及材料特性的影响。此外,针对本文数值分析中出现了a/t较小时约束因子先增大在降低的现象,而Guo方法结果变化趋势不明显,说明本文方法能够更好地反映表面裂纹尺寸和形状综合作用的影响。
针对表面位置处的约束因子,Guo方法根据式(7)和式(9)可以得到此处等效厚度Beq趋近0,因此约束因子α趋近1。而本文数值分析得到的裂纹表面点处约束因子在1~1.5,且随a/t、a/c和S/σ0变化而变化。可见本文提出的数值方法能更好的反映不同裂纹尺寸、形状和载荷水平下的裂纹前缘实际约束情况。此外,从式(7)可知,Guo方法仅给出了裂纹半轴比a/c≤1情况下的约束因子计算方法,本文数值方法则能进一步考虑a/c>1的情况,具有更广泛的裂纹形状适用性。
上述对比研究表明,程序化仿真计算方法解决了裂纹前缘三维约束因子大量、快速计算的问题,同时具有精度高和适用性广的特点。
4、结论
本文利用弹塑性有限元方法对发动机转子用TC4钛合金表面裂纹前缘三维约束因子分布特性进行了研究,得到以下结论:
(1)表面裂纹前缘约束因子呈“倒U型”分布,从试样表面位置到最深位置,约束效应由近平面应力状态(α≈1.25)转变为近平面应变状态(α≈2.5)。裂纹表面点处约束因子随着裂纹尺寸、裂纹形状以及外加载荷的变化不明显。裂纹最深点处约束因子随外加载荷和裂纹尺寸的增大而减小,受裂纹形状变化影响较小。等值线图表明,裂纹前缘约束因子受裂纹尺寸、裂纹形状以及外加载荷耦合作用,未表现出明显的、单调的变化趋势。
(2)对比研究了Guo方法和本文数值计算方法获得的表面裂纹三维约束因子,结果表明有限元数值仿真更能反映局部应力、裂纹形状以及材料特性的影响,且能表征表面点处的约束因子分布。
在航空发动机钛合金寿命限制件的疲劳裂纹扩展研究中,可以利用本文建立的程序化分析方法,首先计算得到不同形状和尺寸的裂纹前缘三维约束因子分布;然后结合疲劳裂纹闭合模型计算裂纹有效应力强度因子范围;进而基于有效应力强度因子范围为驱动力的裂纹扩展速率方程,进行裂纹前缘不同位置处的扩展预测;最终实现考虑三维裂纹前缘变约束效应的航空发动机钛合金转子寿命限制件的裂纹扩展寿命预测,并为最终的损伤容限评估提供支撑。
在后续的研究中,可进一步开展不同材料、裂纹形状和加载载荷下的约束因子计算分析,建立基础数据库,进而发展基于数据驱动的快速、实用、高精度的计算模型,以便于在工程实践中应用。致谢:感谢国家自然科学基金和浙江省自然科学基金的资助。
参考文献
[1] US Department of Transportation Federal Aviation Administration, Advisory Circular 33.70-1: Guidance material for aircraft engine-life-limited parts requirements[S], Washington DC, US, FAA, 2009.
[2] 中国民用航空局.航空发动机适航规定(CCAR-33R2) [S].北京:中国民用航空局, 2016.
[3] 丁水汀, 周惠敏, 刘俊博, 等. 航空发动 机限寿件表面特征概率损伤容限评估[J]. 航空动力学报, 2021,36(2):421-430.
DING S T, ZHOU H M, LIU J B, et al. Probabilistic damage tolerance assessment of surface features of aero engine life limited parts[J]. Journal of Aerospace Power, 2021,36(2):421-430. (in Chinese)
[4] DANIEWICZ S R. A modified strip-yield model for prediction of plasticity-induced closure in surface flaws[J]. Fatigue & Fracture of Engineering Materials & Structures, 1998(21):885-901.
[5] TORIBIO J, MATOS J C, GONZÁLEZ B. Aspect ratio evolution associated with surface cracks in sheets subjected to fatigue[J]. International Journal of Fatigue, 2016,92:588-595.
[6] TORIBIO J, MATOS J C, GONZÁLEZ B. Aspect ratio evolution in embedded, surface, and corner cracks in finite-thickness plates under tensile fatigue loading[J]. Applied Sciences, 2017,7(7):746.
[7] CORBANI S, CASTRO J T P, MIRANDA A C O, et al. Crack shape evolution under bending-induced partial closure[J]. Engineering Fracture Mechanics, 2018,188:493-508.
[8] ZHAO J H, GUO W L, SHE C M. Three-parameter approach for elastic-plastic fracture of the semi-elliptical surface crack under tension[J]. International Journal of Mechanical Sciences, 2008,50(7):1168-1182.
[9] ZHAO J H, GUO W L. Three-parameter KT-Tz characterization of the crack-tip fields in compact-tension-shear specimens[J]. Engineering Fracture Mechanics, 2012,92:72-88.
[10] CUI P F, GUO W L. Higher order J-T-A solution for three-dimensional crack border fields in power-law hardening solids[J]. Engineering Fracture Mechanics, 2019,222:106736.
[11] CUI P F, GUO W L. Crack-tip-openingdisplacement-based description of threedimensional elastic-plastic crack border fields[J]. Engineering Fracture Mechanics, 2020,231:107008.
[12] 郭万林, 许磊, 周正. 三维计算断裂力学[J]. 计算力学学报, 2016,33(4):431-440.
GUO W L, XU L, ZHOU Z. Computational mechanics of three-dimensional fracture[J]. Chinese Journal of Computational Mechanics, 2016,33(4):431-440. (in Chinese)
[13] WILLIAMS M L. On the stress distribution at the base of a stationary[J]. Journal of Applied Mechanics, 1957,24:109-114.
[14] O'DOWD N P. Applications of two parameter approaches in elastic-plastic fracture mechanics[J]. Engineering Fracture Mechanics, 1995,52(3): 445-465.
[15] GUO W L. Three-dimensional analyses of plastic constraint for through-thickness cracked bodies[J]. Engineering Fracture Mechanics, 1999,62(4):383-407.
[16] YU P S, GUO W L. An equivalent thickness conception for prediction of surface fatigue crack growth life and shape evolution[J]. Engineering Fracture Mechanics, 2012,93:65-74.
[17] YU P S, GUO W L. An equivalent thickness conception for evaluation of corner and surface fatigue crack closure[J]. Engineering Fracture Mechanics, 2013,99:202-213.
[18] ZHAO J H, GUO W L, SHE C M, et al. Three dimensional K-Tz stress fields around the embedded center elliptical crack front in elastic plates[J]. Acta Mechanica Sinica, 2006,22(2):148-155.
[19] GUO W, ZHU J C, GUO W L. Equivalent thickness-based three dimensional stress fields and fatigue growth of part-through cracks emanating from a circular hole[J]. Engineering Fracture Mechanics, 2020,228:106927.
[20] MOSTAFAVI M, SMITH D J, PAVIER M J. Reduction of measured toughness due to outof-plane constraint in ductile fracture of aluminium alloy specimens[J]. Fatigue & Fracture of Engineering Materials & Structures, 2010,33(11):724-739.
[21] YANG J. Unified correlation of constraint and strength mismatch with fracture toughness of bimetallic joint[J]. Procedia Engineering, 2015,130:853-860. [22] 徐建勇, 王国珍, 轩福贞,等. 基于裂尖张 开位移的统一拘束参数与材料断裂韧性 的关联[J]. 压力容器, 2018,35(11):16-22.
XU J Y, WANG G Z, XUAN F Z, et al. Correlation of unified constraint parameter based on CTOD with fracture toughness of material[J]. Pressure Vessel Technology, 2018,35(11):16-22. (in Chinese) [23] NEWMAN J C. A crack-closure model for predicting fatigue crack growth under aircraft spectrum loading[M]. West Conshohocken, PA: ASTM International, 1981.
[24] MACHNIEWICZ T. Fatigue crack growth prediction models for metallic materials Part II: Strip yield model - choices and decisions[J]. Fatigue & Fracture of Engineering Materials & Structures,2013,36(4):361-373.
[25] NEWMAN J C, BIGELOW C A, SHIVAKUMAR K N. Three-dimensional elastic-plastic finite-element analyses of constraint variations in cracked bodies[J]. Engineering Fracture Mechanics, 1993, 46(1):1-13.
[26] GUO W L, WANG C K, ROSE L R F. The influence of cross-sectional thickness on fatigue crack growth[J]. Fatigue & Fracture of Engineering Materials & Structures, 1999,22(5):437-444. [27] WANG G S, BLOM A F. A strip model for fatigue crack growth predictions under general load conditions[J]. Engineering Fracture Mechanics, 1991,40(3):507-533.
[28] MCMASTER F J, SMITH D J. Predictions of fatigue crack growth in aluminium alloy 2024-T351 using constraint factors[J]. International Journal of Fatigue, 2001,23:93- 101.
[29] 吴连生, 于培师, 韦朋余, 等. 基于三维 理论的 TC4ELI 钛合金疲劳裂纹扩展研究[J]. 船舶力学, 2022,26(9):1354-1362.
WU L S, YU P S, WEI P Y, et al. Fatigue crack growth of TC4ELI titanium alloy based on three-dimensional theory[J]. Journal of Ship Mechanics, 2022,26(9):1354-1362. (in Chinese)
[30] 许磊. 基于裂纹闭合模型的三维裂纹疲劳 扩展分析[D].南京:南京航空航天大学, 2018. XU L. Three-dimensional fatigue crack growth analysis based on crack closure model[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. (in Chinese)
[31] 周斌. 某镍基粉末高温合金三维裂纹扩展 试验与分析研究[D].南京:南京航空航天 大学, 2022.
ZHOU B. Experimental and analysis study on three-dimensional crack growth of a Nickel-base powder superalloy[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2022. (in Chinese)
[32] HUANG X N, CHEN C Y, XUAN H J. Experimental and analytical investigation for fatigue crack growth characteristics of an aero-engine fan disc[J]. International Journal of Fatigue, 2021,148:106252.
[33] MCCLUNG R C, LEVERANT G R, ENRIGHT M P, et al. Turbine Rotor Material Design: Phase II[R]. Washington, DC: Federal Aviation Administration, Department of Transportation, 2008.
[34] DANIEWICZ S R, AVELINE C R. Stripyield and finite element analysis of partthrough surface flaws[J]. Engineering Fracture Mechanics, 2000,67(1):21-39.
tag标签:钛合金



