发布日期:2025-12-20 15:34:23
引言
钛合金以其卓越的高比强度、优异的耐腐蚀性、出色的低温性能及良好的焊接性能,在深海环境结构中占据了举足轻重的地位 [1],特别是Ti6Al4V ELI钛合金展现了其独特的材料优势,广泛应用于载人潜水器的球舱制造中 [2]。然而,深海服役的钛合金结构需同时承受巨大的静水压力和复杂的交变载荷,这些因素极易诱发微小裂纹的萌生并推动其扩展,对深海结构的长期稳定性和安全性构成了严峻挑战。在钛合金结构的疲劳寿命中,裂纹萌生阶段占据了绝大部分 [3]。因此,深入探究Ti6Al4V ELI钛合金构件的疲劳裂纹萌生寿命,对于精确评估服役环境下钛合金结构的使用寿命,以及科学制定其安全检查周期具有重要意义。
目前,针对Ti6Al4V ELI钛合金疲劳寿命分析的方法主要分为两类:①基于疲劳累积损伤理论的疲劳安全寿命计算方法;②基于线弹性断裂力学的损伤容限计算方法。疲劳安全寿命计算方法利用简单试件的应力 - 寿命曲线进行构件寿命估算。高焱等 [4] 基于机械工程研究协会疲劳强度设计规范 FKM (Forschungs Kuratorium Maschinenbau) 得到了适用于增材制造 TA15 钛合金结构的疲劳寿命计算方法,且计算精度较好。LIN 等 [5] 的研究表明,与应力 - 寿命评估方法相比,应变 - 寿命方法能够更准确地描述结构在周期性过载下的局部塑性变形。损伤容限计算方法是基于线弹性断裂力学建立的,该方法对于稳定扩展阶段的长裂纹扩展寿命预测比较准确。吴连生等 [6]、ZHAO 等 [7]、BIAN 等 [8]、YU 等 [9-10]、陶蒙等 [11] 在三维断裂理论框架下,实现了不同厚度Ti6Al4V ELI钛合金试件在不同载荷下的疲劳裂纹扩展寿命和裂纹长度的准确预测,提高了深海耐压结构的损伤容限设计精度。张海英等 [12] 通过试验获取了不同状态激光选区熔化 Ti6Al4V 钛合金的裂纹扩展性能数据,证明了超过一定范围的裂纹尺寸和应力强度因子会导致表面机械加工处理对裂纹扩展性能几乎无影响。WANG 等 [13] 对深海载人潜水器中使用的Ti6Al4V ELI钛合金进行了结构级驻留疲劳试验,验证了载人潜水器压力舱体在驻留疲劳载荷下的结构完整性。然而,当前针对Ti6Al4V ELI钛合金疲劳寿命预测的研究仍存在一定的局限性。疲劳安全寿命计算易受结构几何参数、连接方式、工艺方法及加载顺序等多重因素的影响,导致预测结果出现偏差。而损伤容限计算方法则无法涵盖裂纹萌生阶段的寿命预测。CHAN [14] 通过大量试验和数值模拟发现,材料微结构对于疲劳裂纹的萌生和扩展起着重要的作用,如晶粒尺寸的均匀性很大程度上会影响材料的疲劳寿命。Ti6Al4V ELI 钛合金结构的裂纹萌生寿命深受材料微观结构特征和局部应力状态的共同影响,它们在结构微缺陷和微裂纹的损伤及演化过程中起重要作用,使得在宏观特性和载荷水平相同的情况下,不同微结构试件的疲劳寿命呈现出显著的差异性。因此,需要采用晶体塑性 (Crystal Plasticity, CP) 有限元模型来模拟微观结构对材料疲劳寿命的影响。在晶体塑性理论中,晶体材料的塑性变形主要源自滑移面上的位错滑移。通过预设晶粒尺寸的成核与生长关系,在不均匀微观结构中对有限小裂纹的扩展进行模拟,从而可以较为准确地估计初始裂纹的分布情况。这种方法不仅能够精确预测裂纹的萌生过程,还能够深入揭示材料疲劳破坏的微观机制 [15]。
为了准确预测裂纹萌生寿命,需要引入疲劳指示因子 (Fatigue Indicator Parameter, FIP),并将其与疲劳裂纹萌生相关的微观力学行为和驱动力紧密联系起来。自 MANONUKUL 等 [16] 在 2004 年提出晶体塑性有限元框架下的 FIP 概念以来,该领域取得了快速发展,形成了多种基于累积塑性滑移 (Plastic Strain Accumulation, PSA)、应变能耗散 [17]、应变统计学理论 [18] 及驻留滑移带能量 [19] 的疲劳指示因子。其中,累积塑性滑移 [20-23] 和累积能量耗散 [24] 是 2 种应用较多的疲劳指示因子。MCDOWELL 等 [25-27] 引入 FIP,将细观力学与基于微观结构的驱动力结合,描述晶粒疲劳裂纹萌生行为。LIU 等 [28] 将对 TC4 合金的试验与晶体塑性理论相结合,得出柱面滑移处高度累积的塑性应变和应力集中导致裂纹萌生,裂纹通常在界面处成核的结论。然而,现有的预测模型大多聚焦于均匀晶粒结构,忽视了真实微观结构的复杂性,这导致预测结果与实际情况之间存在显著差异。因此,有必要通过电子背散射衍射 (Electron Back Scatter Diffraction, EBSD) 技术重构Ti6Al4V ELI钛合金的真实微观结构,并在此基础上建立晶体塑性有限元模型。
针对具有双相组织的Ti6Al4V ELI钛合金,运用 EBSD 技术构建了一个基于其真实微观结构的晶体塑性循环本构模型。为了更精确地评估微观短裂纹的成核寿命,模型采用了累积塑性滑移和累积能量耗散 2 种疲劳指示因子。首先,本文对光滑试样开展了单轴拉伸试验和疲劳试验。其次,将试验结果与有限元模拟结果进行比较,确定了晶体塑性模型中的关键参数,包括初始硬化模量和临界分解切应力等,这些参数的精确获取为后续的疲劳寿命预测奠定了坚实的基础。随后,利用疲劳指示因子与循环次数之间存在的近似线性关系,对不同微结构Ti6Al4V ELI钛合金试样在不同应变幅下的疲劳裂纹萌生寿命进行了预测。最后,将预测结果与经典的 Coffin-Manson (C-M) 定律进行了对比分析。强调了考虑材料微观结构在疲劳寿命预测中的重要性,建立的晶体塑性循环本构模型在揭示材料疲劳行为微观机制方面展现了独特优势。这一研究旨在更深入地探索Ti6Al4V ELI钛合金的疲劳裂纹萌生寿命,从而为其耐久性和结构安全性提供有力支持。
1、试验设计
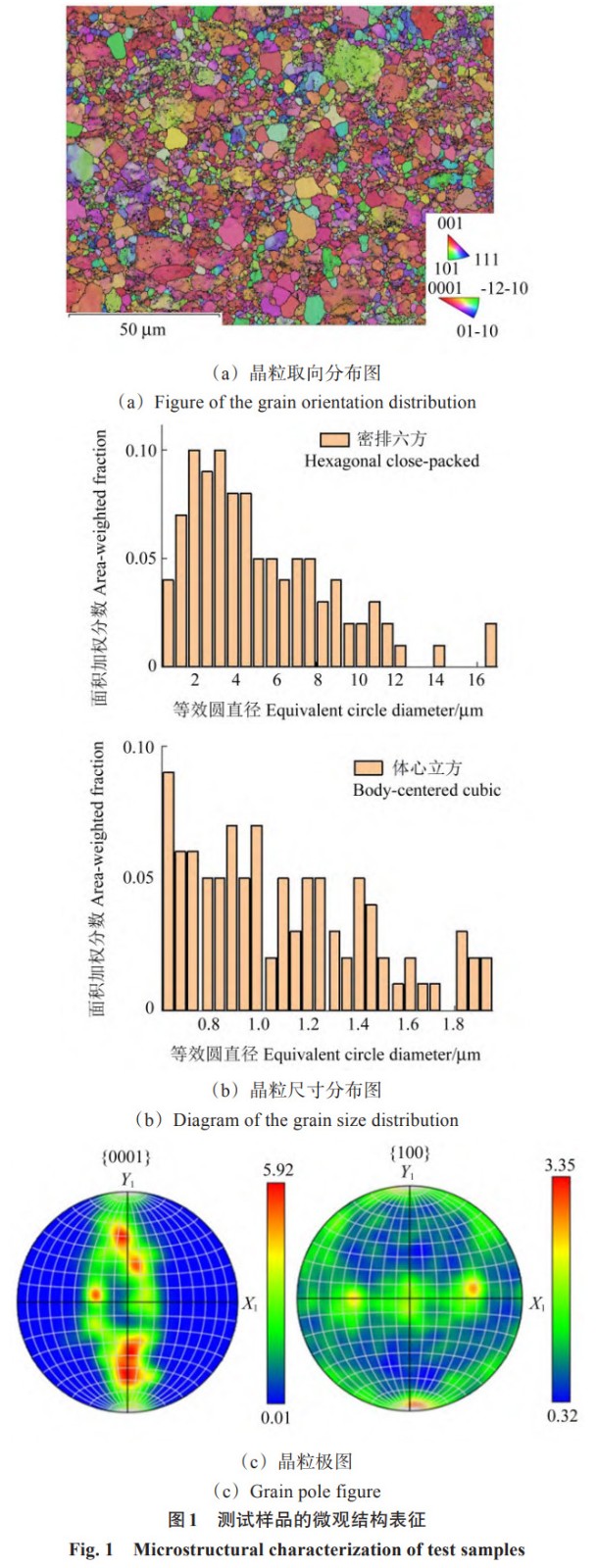
本试验选用具有高损伤容限性能的Ti6Al4V ELI钛合金。为了获取Ti6Al4V ELI钛合金的真实微观结构和力学参数,采用 EBSD 技术对在不同应变加载条件下的试件进行微观结构表征,并建立与其对应的晶体塑性有限元模型。根据样品表面质量,选择的扫描波束电压为 20 kV,工作距离为 15 mm,倾斜角度为 70°,总扫描时间为 45 min,放大倍率为 1000。经过 EBSD 测试,获得了样品的显微组织信息。图 1 (a)~ 图 1 (c) 分别为晶粒的取向分布图、尺寸分布图及极图。
使用图 2 (a) 所示的 MTS Landmark 370.10 型试验机对Ti6Al4V ELI钛合金进行准静态单轴拉伸试验和疲劳裂纹萌生试验。Ti6Al4V ELI 钛合金的元素组成如表 1 所示。在单轴拉伸试验中,加载速度设定为 3 mm/min,并使用常温引伸计来精确测量试样在拉伸过程中所经历的变形。为确保结果的可靠性,试验选取 3 块试样进行重复拉伸试验。同时,针对含有预设缺口的试样,进行了疲劳裂纹萌生试验。该试验中,加载频率设定为 8 Hz,载荷可用三角波形加载幅值曲线描述,并确保应变比为 0。为了深入探究不同应变幅值对Ti6Al4V ELI钛合金疲劳裂纹萌生寿命的具体影响,本文设计了多组疲劳裂纹萌生试验,各组的应变 (ε) 分别为 0.5%、0.55%、0.6%、0.65%、0.7% 及 0.75%。
依照标准 GB/T 228.1-2021 [29],设计了图 2 (b) 和图 2 (c) 所示的板状结构试样。这些试样通过精密的线切割技术加工而成,具体分为单边缺口拉伸 (Single Edge Notch Tension, SENT) 试样和无缺口试样 2 种类型。图 2 (b) 为含缺口试样,用于评估Ti6Al4V ELI钛合金在不同应变条件下的裂纹萌生寿命。图 2 (c) 为无缺口试样,其主要用于校准和验证仿真模型的参数。在试验准备阶段,首先在试件表面均匀喷涂一层白色油漆,以增强裂纹的可视性。随后,使用菲林尺配合数字显微镜对缺口部位进行细致观察,这一步骤对于准确监测裂纹的起裂位置和测量裂纹长度至关重要。为了精确获取含缺口试样的裂纹萌生寿命,试验采取定期中断的策略,即每当达到一定的循环次数后,试验会暂停,并施加一个相当于 80% 最大水平应变的静态拉伸载荷。这一操作有助于清晰地暴露出潜在的裂纹。接着,利用数码显微镜仔细观察缺口处的裂纹形态,并通过菲林尺精确测量裂纹的长度,其测量范围设定为 0~0.3 mm。与此同时,详细记录当前应变每个裂纹长度所对应的循环次数,从而为后续的裂纹萌生寿命分析提供准确的数据。
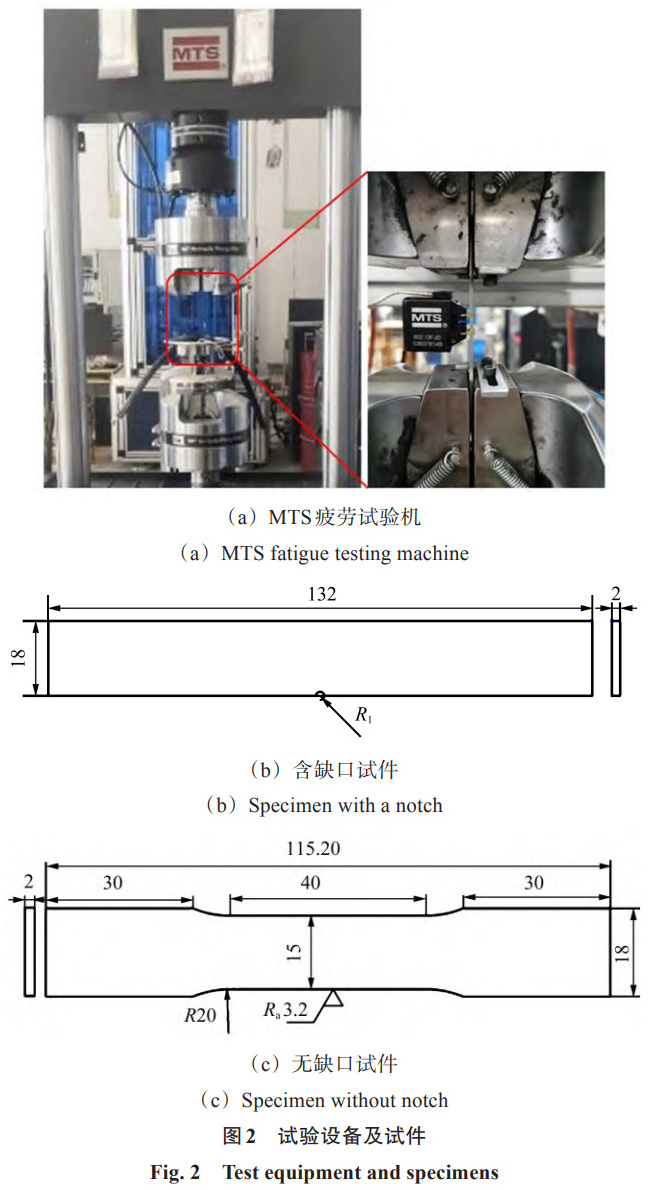
表 1Ti6Al4V ELI钛合金的元素组成
Tab. 1 Elemental composition of theTi6Al4V ELItitanium alloy(%)
| Ti | Al | V | Fe | O | N | C | H |
| 余量 Balance | 6.2 | 4.2 | 0.046 | 0.12 | 0.008 | 0.0013 | 0.0045 |
2、晶体塑性理论
本文采用率相关晶体塑性本构模型,其本构方程主要描述了塑性变形过程中剪切速率与剪切应力之间的关系。滑移系统的变形是由分解切应力驱动的。晶体材料的总变形梯度 F 的表达式 [30] 为:

式中, F e 为由于晶格点阵的拉伸和扭曲而产生的弹性变形梯度; F p 为由于晶体滑移而引起的塑性变形梯度。塑性速度梯度 L p 与滑移系 α 上的滑移率 γ ˙ α 的关系式为:
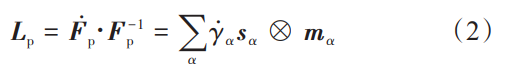
式中, s α 为滑移方向; m α 为滑移面法向。塑性变形是由各个滑移系下的剪切变形贡献得到的。根据 Schmid 定律,当分解切应力的大小超出临界值 (临界分解切应力) 时,滑移系统将被激活。晶体滑移系上分解切应力 τ α 的表达式为:
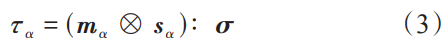
式中,σ 为 Cauchy 应力张量。在晶体发生塑性变形时,滑移系开动以及滑移时产生的滑移剪切速率 γ ˙ α 可根据黏塑性幂法则计算 [31],即:
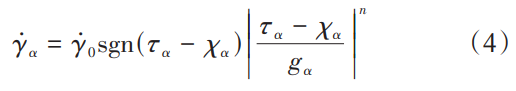
式中, γ ˙ 0 为参考塑性滑移率; χ α 为背应力; g α 为某一时刻滑移系的应变硬化强度;n 为速率敏感指数,当 n 趋于无穷时,上述方程是率无关的。参数 g α 可表征材料的应变硬化过程,其变化率 g ˙ α 的表达式为:

式中, h αβ 为自硬化模量 (α=β) 或潜硬化模量 (α≠β); γ ˙ β 为滑移系 β 上的滑移率。潜硬化模量可表示为:
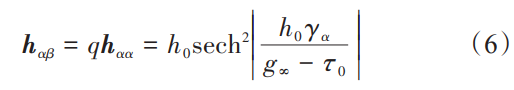
式中,q 为常数; h 0 、 τ 0 和 g ∞ 分别为初始硬化模量、临界分解切应力和饱和应力,且均为材料常数; γ α 为滑移剪切应变。
γ 为所有滑移系上的累积剪切应变,即滑移率 γ ˙ 随时间 t 的积分,可表示为:

式 (4) 中,运动硬化的背应力χα遵循非线性演化规律,即:
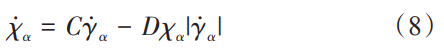
式中,C、D 分别为描述滑移系线性、非线性硬化特性的材料常数。累积塑性滑移已被证明与循环变形过程中的疲劳损伤密切相关,因此常作为疲劳指示因子,用于预测低周疲劳裂纹萌生寿命。累积塑性滑移 [32] 为:

其中,
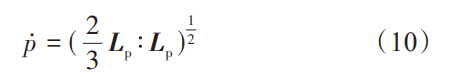
当累积塑性滑移达到临界值pcrit时,疲劳裂纹萌生。
pcrit满足的关系式为:

式中,Ni为从试验中获得的低周疲劳 (Low Cycle Fatigue, LCF) 裂纹长度 0~0.3 mm 对应的循环次数,近似等于 LCF 裂纹萌生寿命;pcycj为每循环下的预测塑性应变增量。
此外,累积能量耗散 W 是评估疲劳裂纹萌生的另一种疲劳指示因子,表示为:
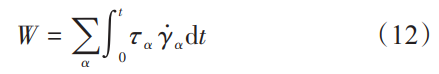
与累积塑性滑移类似,累积能量耗散临界值Wcrit满足的关系式为:

3、有限元仿真
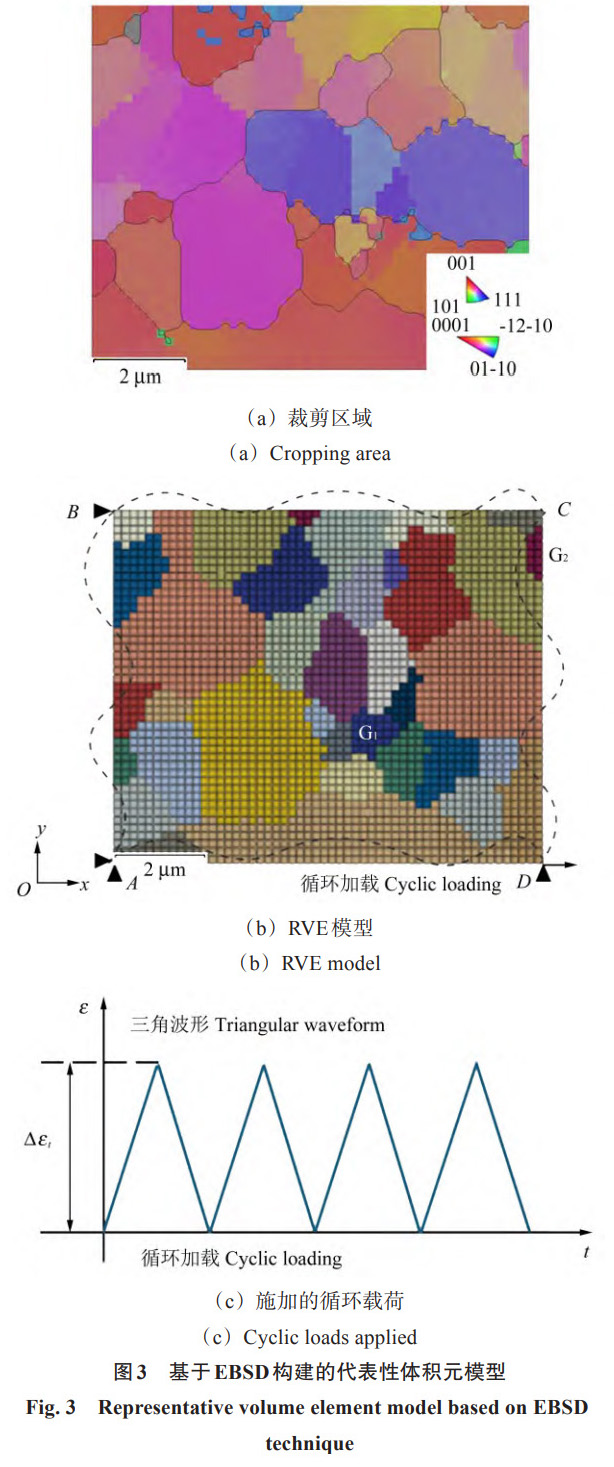
基于真实微观结构的模型能够精确地再现Ti6Al4V ELI钛合金的实际微观结构特征、形貌以及晶粒间的不均匀性,这对于准确描述其低周疲劳损伤行为至关重要。为了在保证模拟精度的同时降低计算复杂度,模型采用 EBSD 数据后处理软件 Aztec Crystal,从图 1 (a) 所示的真实双相微观结构图像中裁剪出一个尺寸为 9.6 μm×8.0 μm 的代表性区域,如图 3 (a) 所示。随后,利用 Matlab 软件中的 MTEX 工具箱,基于该裁剪后的区域构建一个二维的代表性体积元 (Representative Volume Element, RVE) 模型,用于深入研究循环加载下材料的变形行为。图 3 (b) 为采用 C3D8 单元对 RVE 几何模型进行细致的离散化处理。根据 EBSD 的结果,将 RVE 中的晶粒G1和G2指定为 β 相,而其余的晶粒则统一归类为 α 相,并使用 Python 脚本为所有晶粒随机分配了取向。由于 RVE 模型在宏观尺度上可以视为一个物质点,因此为其施加了周期性边界条件,并在 D 点施加循环位移载荷,如图 3 (b) 所示。这样设计是为了模拟材料在真实环境中的受力情况。图 3 (c) 为所施加的三角波循环载荷,其中应变比均设为 0,以确保试验条件的一致性。
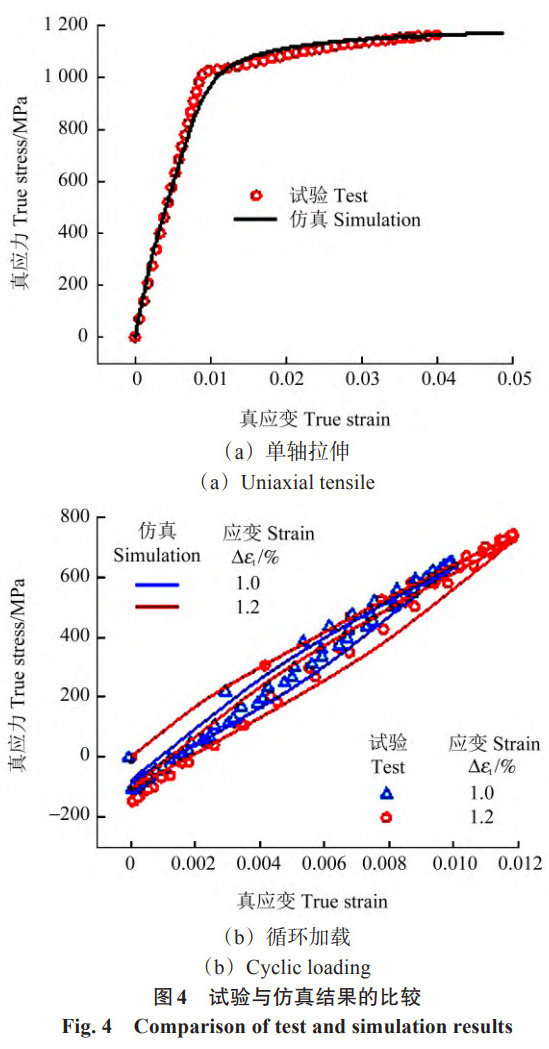
为了精确获取Ti6Al4V ELI钛合金在晶体塑性模拟中所需的参数,对试件进行了一系列单轴拉伸试验以及不同应变 (Δεt) 的低周疲劳试验。图 4 为试验结果与仿真结果的对比。由图 4 可知,无论是单轴拉伸还是循环加载,有限元仿真得到的应力 - 应变曲线都与试验结果保持了高度的一致性。这里所提及的应力与应变为真应力、真应变。利用试验中获得的名义应力和名义应变,通过方程σtrue=σe(1+εe)可得到相应的真应力。试验和仿真结果的一致性不仅彰显了仿真的精确性,也充分验证了所选用材料参数的有效性和可靠性。
从基于试验所得的应力 - 应变曲线中,可得出一系列关键参数,包括初始硬化模量h0、饱和应力g∞、临界分解切应力τ0以及与背应力相关的 C、D 参数,部分参数值如表 2 所示。对于 α 相的晶体塑性参数,参考了 BALASUBRAMANIAN 等 [33] 的研究成果;而对于 β 相的参数,则参考了 OGI 等 [34] 和 HE 等 [35] 的研究数据。在仿真过程中,设定试样的参考塑性滑移率γ˙0为0.001s−1,滑移自硬化与潜硬化效应的比值 q 为 1.0,与背应力相关的 C、D 参数分别为 500、50。
表 2 α 相和 β 相的材料常数
Tab. 2 Material constants of α-phase and β-phase
| 滑移系类型 | 晶面 | h 0 /MPa | τ 0 /MPa | g ∞ /MPa |
| 基面 Basal | {0001} | 605.0 | 390.0 | 400.2 |
| 柱面 Prismatica | {10 1 ˉ0} | 640.0 | 391.0 | 400.2 |
| 锥面 Pyramidal | {10 1 ˉ1} | 645.0 | 391.0 | 400.2 |
| 锥面 |
{10 1 ˉ1} | 650.0 | 391.0 | 400.2 |
| β 相 β-phase | {110} | 150.0 | 80.3 | 99.5 |
表 3Ti6Al4V ELI钛合金的晶格滑移系
Tab. 3 Lattice slip systems of theTi6Al4V ELItitanium alloy
| 滑移系统 Slip system | 晶面 - 晶向 | 数量 Number |
| 基面 Basal | {0001}<11 2 ˉ0> | 3 |
| 柱面 Prismatica | {10 1 ˉ0}<11 2 ˉ0> | 3 |
| 锥面 Pyramidal | {10 1 ˉ1}<11 2 ˉ0> | 6 |
| 锥面 |
{10 1 ˉ1}<11 2 ˉ3> | 12 |
| β 相 β-phase | {110}<111> | 12 |
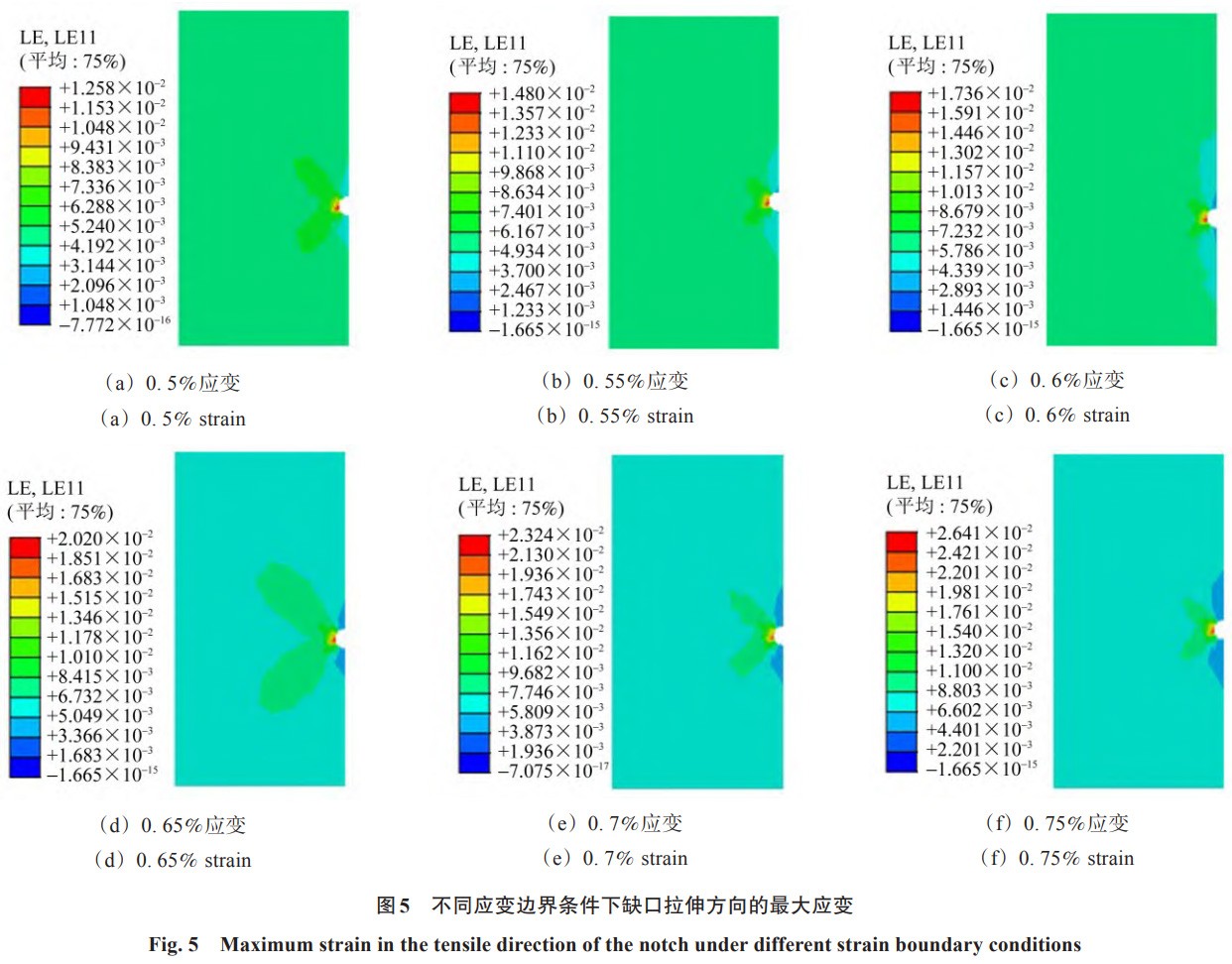
鉴于疲劳试验采用的是带有缺口的试件,并且 EBSD 技术测量的是缺口部位的微观结构,因此必须考虑缺口导致的应变集中对 RVE 模型可能产生的影响。为了精确评估这一影响,结合试验数据构建了一个宏观有限元模型。该模型首先模拟了不同应变条件下,缺口拉伸方向上的最大应变值;随后,将这些模拟得到的最大应变值作为输入条件,应用于 RVE 模型中。为了确保模拟过程能够准确描述材料的力学性能,针对Ti6Al4V ELI钛合金的特性,本研究选择了最为合适的本构模型。通过分析Ti6Al4V ELI钛合金的应力 - 应变曲线,确定了其弹性模量为 121.2 GPa,并采用了指数形式的数学本构模型对其进行描述。该模型的具体表达式为 σ = A ′ + B ′ε z,其中,参数 A ′ = 242.34MPa、 B ′ = 1433.69MPa和 z = 0.128分别为特定温度条件下材料的屈服强度、应变硬化系数以及应变硬化指数。在宏观有限元模型的设置中,对模型的下部在 x、y、z 这 3 个方向均施加了固定约束,对上部则施加了与试验条件相匹配的单轴拉伸应变。模拟的结果如图 5 所示,对于应变值为 0.5%、0.55%、0.6%、0.65%、0.7% 和 0.75% 的试件,其缺口拉伸方向上的最大应变分别达到了 1.26%、1.48%、1.74%、2.02%、2.32% 和 2.64%。
4、模拟结果与讨论
4.1 疲劳损伤
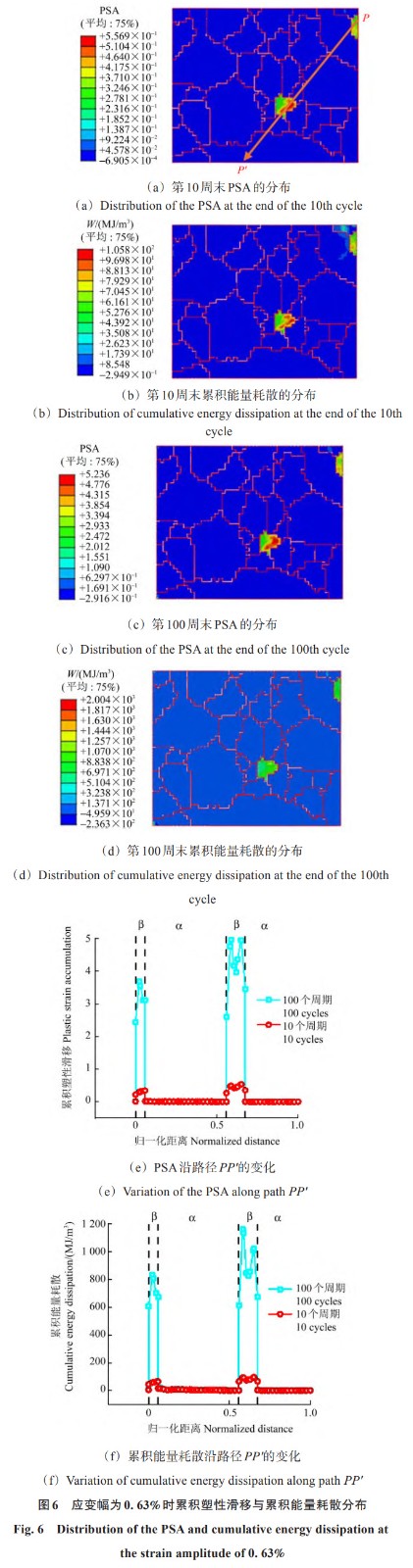
通过 EBSD 试验,构建了反映真实微观结构的 RVE 模型,并利用 Abaqus 有限元分析软件对其进行了循环变形模拟,旨在从微观层面深入探究疲劳损伤的相关因素。图 6 (a) 和图 6 (c) 分别为在应变幅为 0.63% 的条件下,经过 10 周和 100 周循环后 RVE 中的累积塑性滑移分布情况。由图 6 (a)、图 6 (c) 可知,与宏观上的均匀应变状态相比,微观层面上 RVE 内各晶粒的应变呈现出显著的不均匀性,特别是 β 相晶粒更倾向于发生塑性变形。沿路径 PP ′的累积塑性滑移分布进一步揭示了应变主要集中在 α 相与 β 相的界面处,如图 6 (e) 所示。图 6 (e) 中黑色虚线标记的位置为累积塑性滑移的峰值,这暗示了相邻晶粒间滑移阻力的差异是上述现象出现的关键因素。随着循环次数的累积,局部应变呈现出明显的增强趋势,如图 6 (c) 所示。此外,图 6 (b) 和图 6 (d) 分别呈现了相同应变幅下,第 10 周和第 100 周循环后的累积能量耗散分布情况。值得注意的是,累积能量耗散的分布与累积塑性滑移的分布高度相似。在给定应变幅下,累积能量耗散随着循环次数的增加而持续攀升。沿路径 PP ′的累积能量耗散分布趋势与累积塑性滑移分布趋势基本一致,如图 6 (f) 所示,这进一步验证了两者之间的紧密联系。鉴于疲劳裂纹通常倾向于先在应变较高的区域萌生,累积塑性滑移值因此成为评估疲劳损伤的有效指标,能够准确预示裂纹萌生的趋势。图 6 中显示的 α 相与 β 相界面以及 β 相内部较高的累积塑性滑移值预示着这些区域将承受更大的疲劳损伤风险。
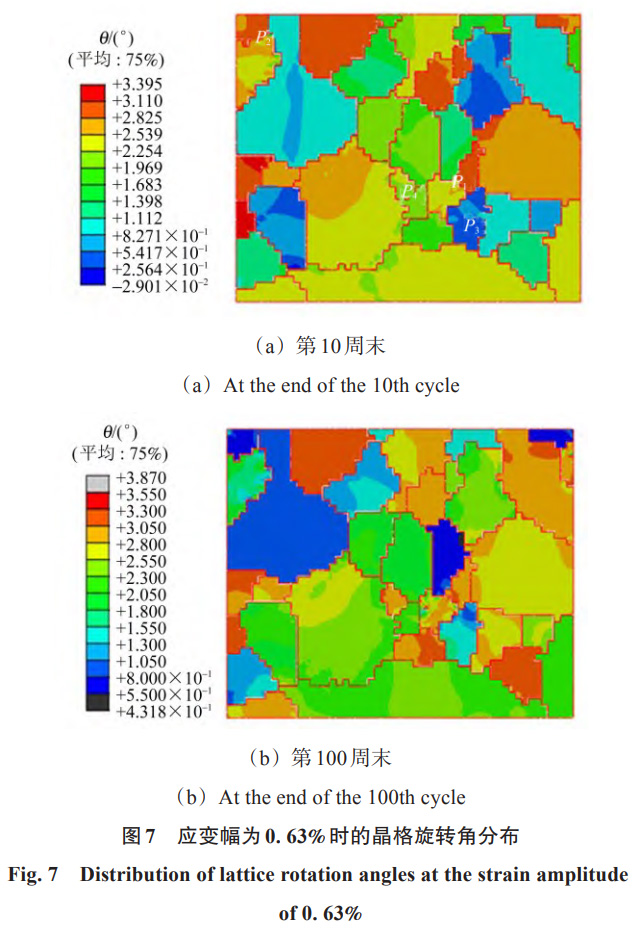
已有研究表明,局部应变往往与微观结构中特定区域的晶格旋转角密切相关 [36]。这种晶格旋转角可通过计算旋转矩阵来确定,具体表达式为θ=π180∘arccos21[trRe−1](Re为晶格旋转矩阵),它反映了晶格结构的局部变化。图 7 (a) 和图 7 (b) 分别为在应变幅为 0.63% 的条件下,经过 10 周和 100 周循环后 RVE 模型中的晶格旋转角分布情况。通过对比分析,发现局部疲劳指示因子与局部晶格旋转之间存在紧密关联:晶格旋转角较大的区域局部疲劳指示因子值也相对较高。晶格的局部旋转不仅导致了微观纹理的形成,还显著提升了裂纹萌生位置的 FIP 值,且在 α 相与 β 相的界面处表现得尤为明显。这一现象清晰地表明,晶格旋转是促使疲劳裂纹萌生以及小裂纹进一步扩展的关键因素之一,这为从微观角度深入理解和预测材料的疲劳行为提供了新的视角和依据。
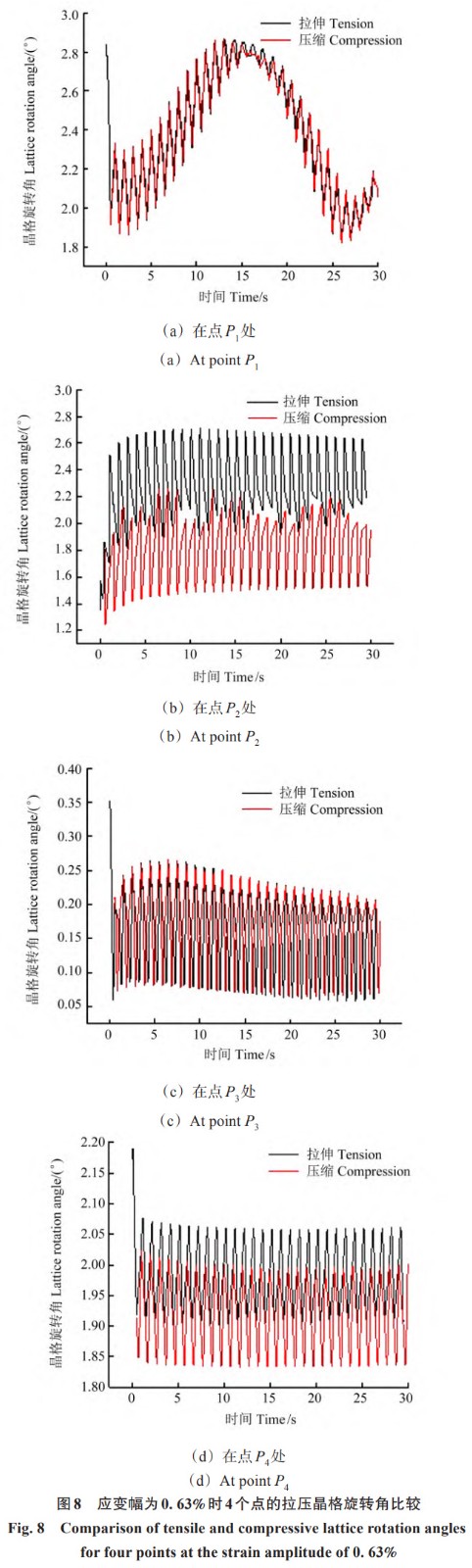
为了更深入地探究疲劳裂纹萌生与局部晶格旋转之间的内在联系,对图 7 (a) 标示的P1、P2、P3和P4这 4 个关键位置的晶格旋转角随时间的变化情况进行进一步分析。图 8 比较了上述 4 个点在连续 30 个拉伸与压缩循环周期中的晶格旋转角变化。由图 8 可知,从第 1 个周期至第 30 个周期,晶格在拉伸与压缩过程中的旋转表现出显著的差异,呈现出明显的拉压不对称性。这种不对称性不仅加速了微观纹理的形成,还进一步加剧了晶格旋转的不均匀性,从而导致了局部区域累积塑性滑移和累积能量耗散的显著增加。换言之,这种拉压不对称的晶格旋转行为是促使局部疲劳损伤加剧的关键因素之一。值得注意的是,每个循环周期内晶格旋转的不对称性还可能引发材料流动行为的拉压不对称性,这将进一步影响材料的整体力学性能和疲劳寿命。
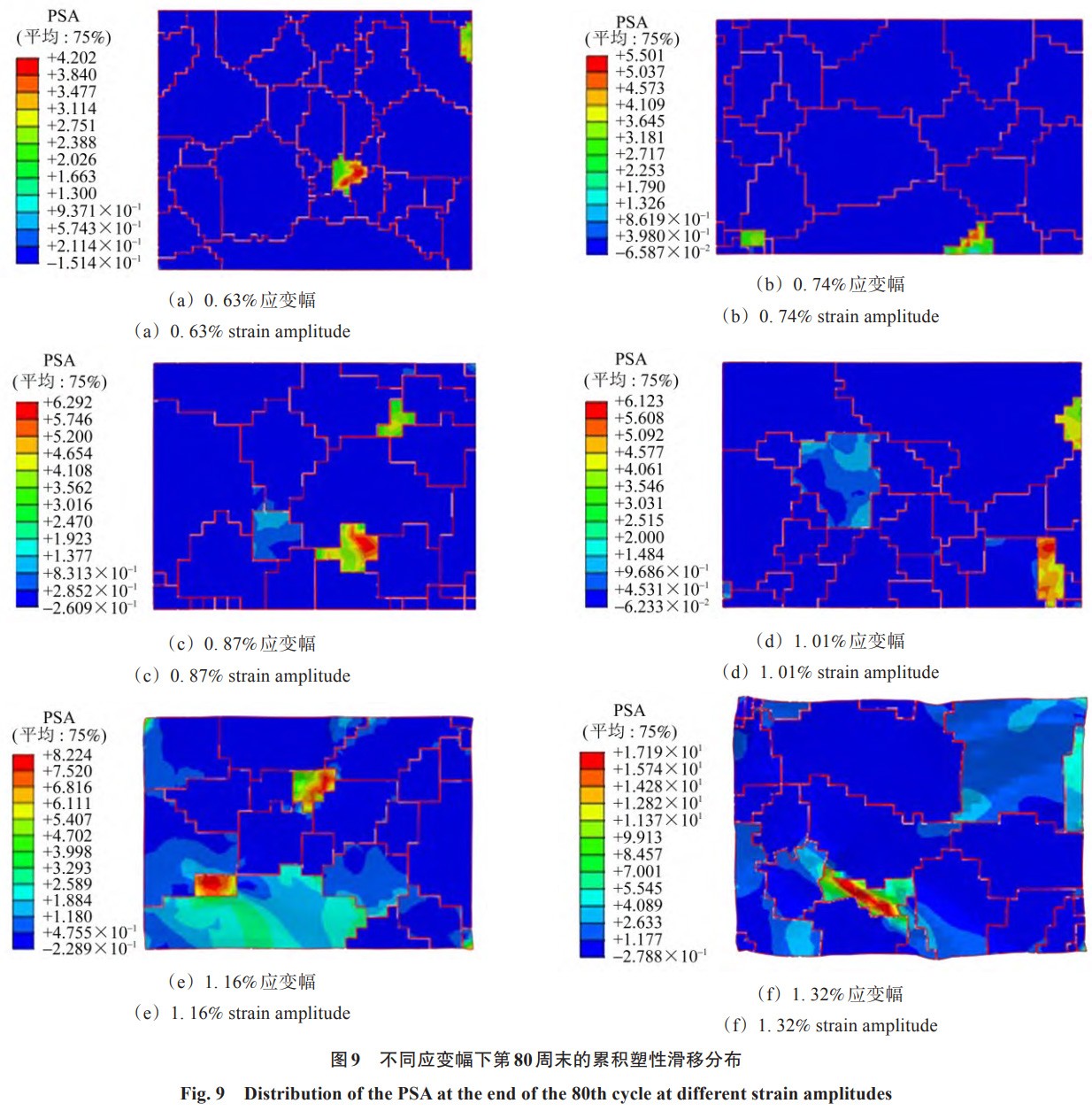
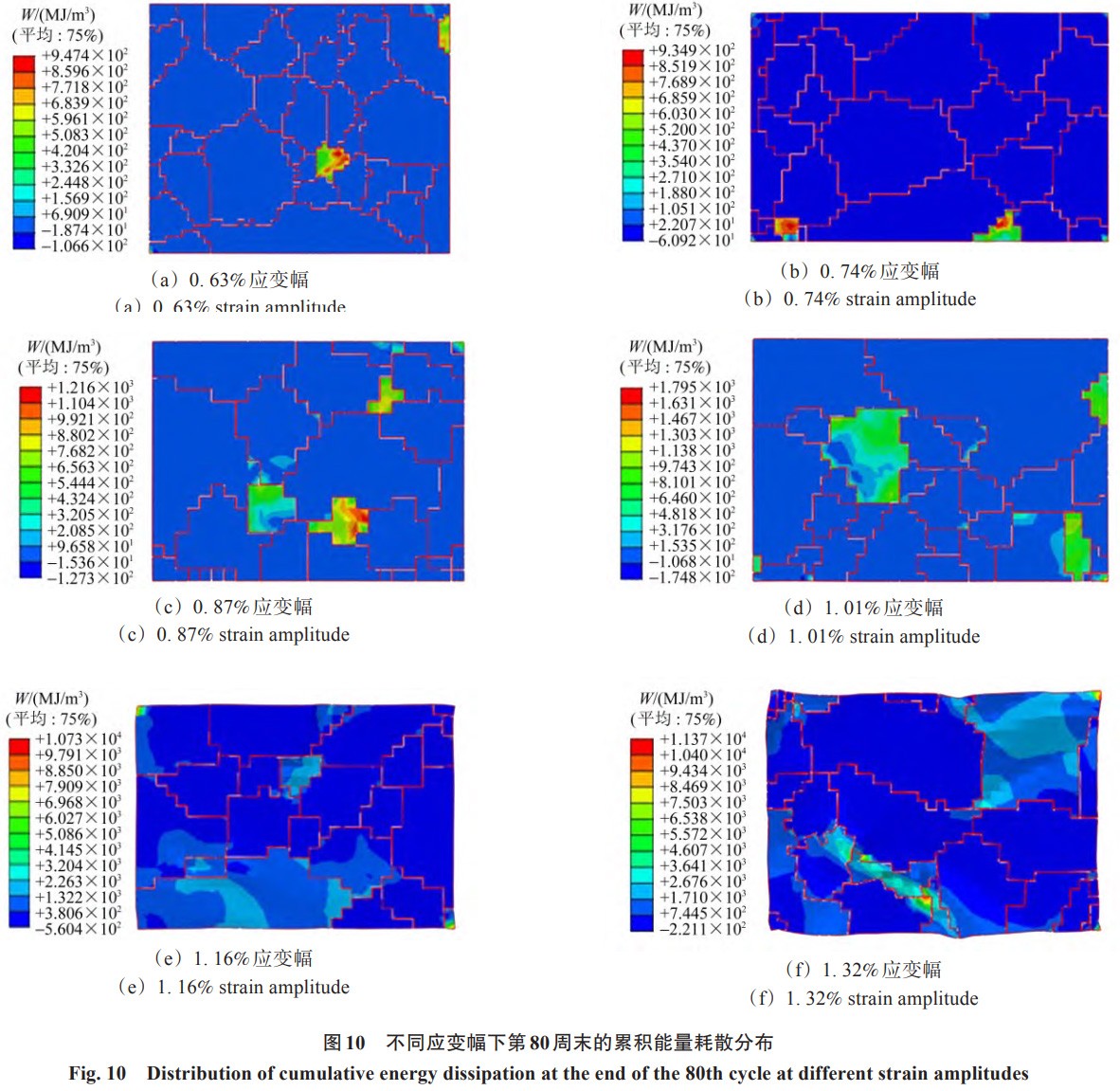
针对不同应变加载条件下的试件,进行了系统的微观结构表征,并结合有限元分析技术开展了深入的模拟研究。图 9 为在不同应变幅下,经过 80 周循环后的累积塑性滑移分布情况。由图 9 可知,随着应变幅的不断增加,累积塑性滑移量大致呈上升趋势。这表明疲劳裂纹萌生的风险也在逐步增加,进而导致材料的疲劳寿命相应缩短。此外,图 10 为在不同应变幅下,经过 80 周循环后的累积能量耗散分布情况。由图 10 可知,累积能量耗散的分布与累积塑性滑移的分布高度一致,从而可将累积能量耗散视为评估疲劳损伤的又一重要指标参数,它能够有效地预测与累积塑性滑移相对应的疲劳裂纹萌生位置。模拟研究的结果进一步证实,无论是基于应变的疲劳指标还是基于能量的疲劳指标,在预测疲劳裂纹萌生位置时均展现出较高的准确性和可靠性。
4.2 疲劳寿命的预测
研究局部疲劳指示因子与循环次数之间的动态关系有助于预测Ti6Al4V ELI钛合金的裂纹萌生寿命。图 11 为累积塑性滑移和累积能量耗散随循环次数递增的变化趋势。由图 11 可知,循环次数与这两者的最大值之间近似成正相关。这一发现为确定如参考塑性滑移率等关键材料参数提供了重要依据。图 11 中的数据均代表整个代表性体积元疲劳指示因子的最大值,这是因为在累积塑性滑移和累积能量耗散达到峰值的区域,材料损伤的风险显著增加。为了更精确地量化这一关系,在应变幅为 0.87% 的条件下,利用试验寿命数据 (Ni) 和模拟至第 40 周末的累积塑性滑移增量 (pcyc),通过式 (11) 得出累积塑性滑移的临界值 (pcrit=311);同样的,利用试验寿命数据 (Ni) 和模拟至第 40 周末的累积能量耗散增量 (Wcyc),依据式 (13) 确定累积能量耗散的临界值 (Wcrit=64374MJ/m3)。
根据试验结果,将含缺口试件在不同应变 (0.5%、0.55%、0.6%、0.65%、0.7% 和 0.75%) 下的裂纹萌生寿命进行了详细记录,其对应的循环次数依次为 6029、5415、3920、3607、3263、2093,如图 12 (a)~ 图 12 (f) 所示。此外,为了更深入地理解疲劳损伤机制,并验证有限元模拟的准确性,本文基于 2 个疲劳指示因子及其临界值对模拟寿命进行了预测,并对试验与模拟 2 种预测方法进行了全面评估。图 13 对比了基于累积塑性滑移模型、累积能量耗散模型和疲劳安全寿命计算方法的疲劳寿命预测结果与低周循环疲劳试验结果。其中,疲劳安全寿命计算依据文献 [37] 中的Ti6Al4V ELI钛合金应变 - 寿命关系式Δεt/2=0.0126(2Nf)−0.080+7.565(2Nf)−1.21,通过线性插值法得出不同应变幅Δε/2下的循环寿命Nrc。对比结果显示,尽管存在一定的误差,但基于两种 FIPs 预测的疲劳寿命呈现出相似的趋势,并且在准确性上高于疲劳安全寿命计算方法。这一发现验证了图 9 和图 10 中累积塑性滑移和累积能量耗散分布的准确性,且符合前述提出的两者在相同位置发生了局部化增强,并且都随着循环次数的增加呈近似线性上升趋势的结论。进一步分析发现,随着应变幅的增加,基于累积塑性滑移的 FIP 相较于基于累积能量耗散的 FIP 表现出更高的预测准确性。
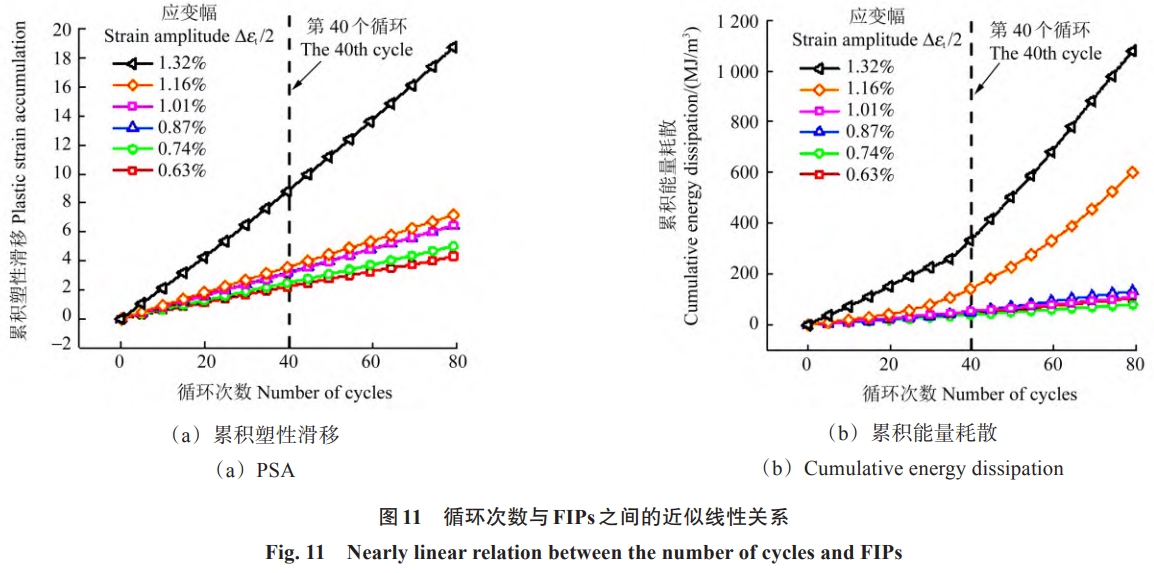

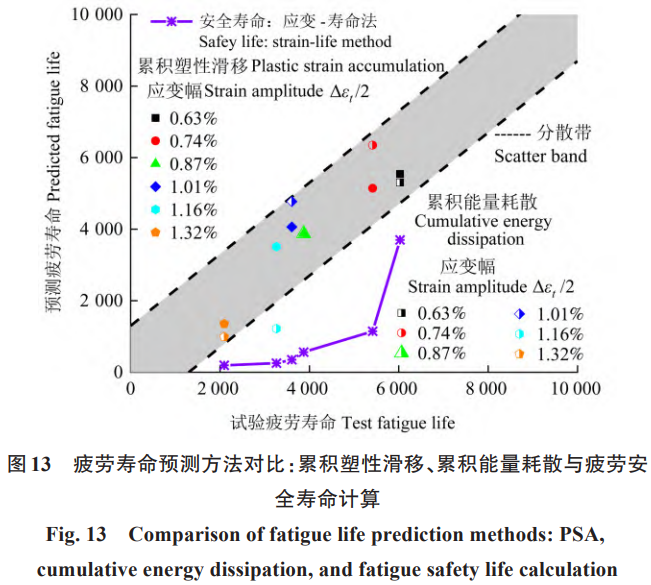
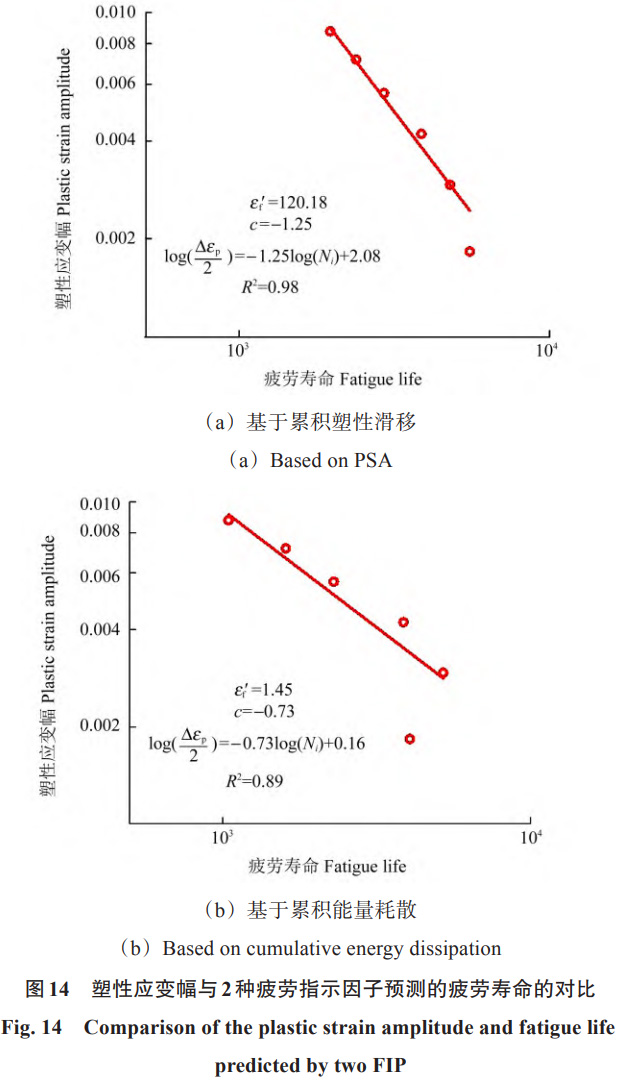
图 14 为塑性应变幅值与基于累积塑性滑移和累积能量耗散这 2 种疲劳指示因子预测的疲劳寿命的对比。在对数坐标系下,这一关系呈鲜明的线性特征。在描述低周循环疲劳寿命Ni时,通常采用 Coffin-Manson (C-M) 定律,该定律将塑性应变幅值Δεp/2通过式Δεp/2=εf′(Ni)c与Ni联系起来,其中εf′为延性系数,c 为疲劳指数。利用 FIP 进行预测的结果揭示了一个重要现象:与宏观 C-M 模型相比,微观结构的不同对材料的裂纹萌生寿命产生了显著影响。这一发现强调了微观结构在疲劳损伤过程中的重要作用。因此在进行疲劳寿命预测时,必须充分考虑材料的微观特征。
4.3 在三维模型中的适用性
探究疲劳指示因子在三维模型中的适用性时,本研究深入分析了晶粒尺寸与网格数量对拉伸应力 - 应变曲线的影响。这对于选定一个既能使模拟曲线与试验数据高度吻合又能确保计算效率的代表性体积元模型至关重要。借助 Neper 建模软件,构建了体积相同但晶粒数量各异的模型,具体涵盖 30、50、100、120 及 150 个晶粒,如图 15 (a) 所示。对比这些多晶体模型的拉伸应力 - 应变曲线,注意到含 30 个与 50 个晶粒的模型的屈服强度与含 100 个以上晶粒的模型存在显著差异。在弹性阶段,所有模型的应力 - 应变曲线近乎重合;然而,步入塑性阶段后,100、120 及 150 晶粒模型的曲线展现出高度的相似性,相比之下,30 与 50 晶粒模型的曲线则明显偏离。基于上述事实,选定 100 晶粒模型,并对其进行了细致的网格敏感性分析。在 Neper 软件中,分别设置模型的网格数量大约为 6 万、10 万、18 万和 46 万,得出不同网格数量的多晶体模型拉伸应力 - 应变曲线,如图 15 (b) 所示。由图 15 (b) 可知,网格数量约为 10 万的晶粒模型的拉伸应力 - 应变曲线呈现出良好的一致性。这一结果意味着,在该网格密度下,模型的计算结果具有较高的稳定性,非常适用于后续的疲劳寿命预测。
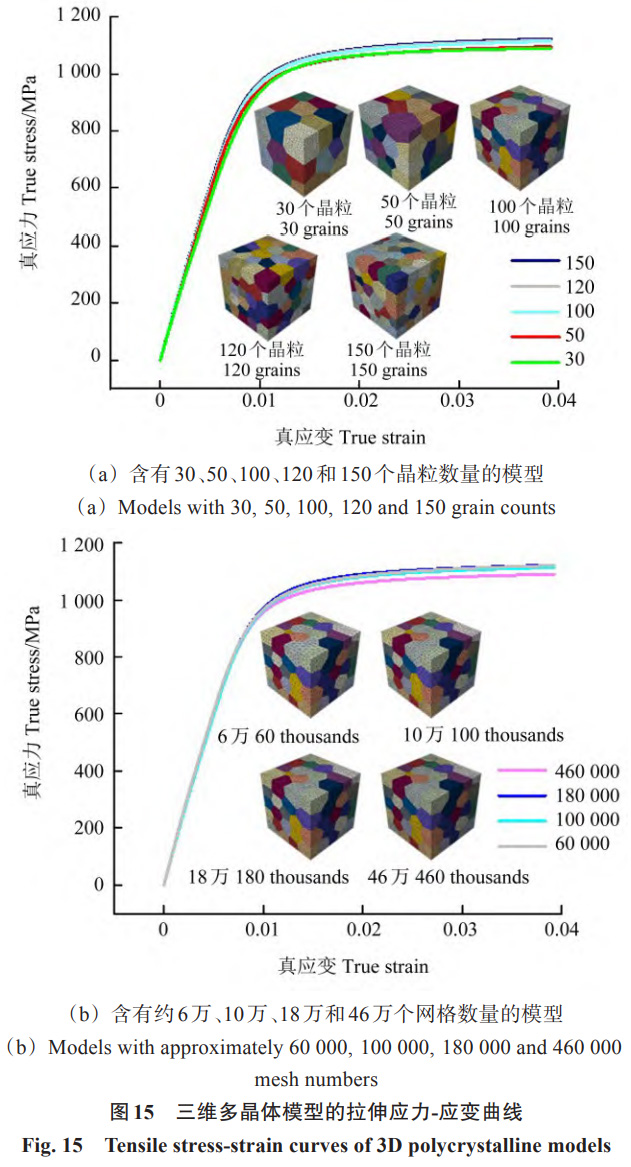
采用 Neper 建模软件,依据 EBSD 获取的晶粒尺寸平均值,构建了三维晶粒随机生长的代表性体积元模型。此模型遵循正态分布原则,标准差设定为 1.23,其中 10% 的晶粒设定为 β 相,其余 90% 则为 α 相。RVE 的边长为 1 mm,内含 100 个晶粒,网格数量调整为约 10 万个,以确保计算效率与精度。为确保计算的连贯性,对 RVE 施加周期性边界条件,以模拟材料的真实变形过程。在此基础上,施加了应变比为 0 的循环位移载荷,并使用第 3 节中确定的材料参数,以深入研究三维结构下的疲劳裂纹萌生寿命。
为分析不同应变幅下疲劳因子在三维结构中的适用性,本节沿用第 3 小节的宏观模拟方法,重新模拟了 0.4% 应变条件下缺口拉伸方向对应的最大应变幅,结果为 0.45%;试验测得的裂纹萌生寿命则为 11908 周。图 16 (a)~ 图 16 (d) 为应变幅值分别为 0.45%、0.63%、0.74% 和 0.87% 时,第 30 周末的累积塑性滑移分布,以表明这些应变幅值下的疲劳损伤情况。同时,图 17 (a)~ 图 17 (d) 为相应应变幅值下第 30 周末的累积能量耗散分布。对比分析可知,随着应变幅值的增加,累积塑性滑移和累积能量耗散均呈显著的上升趋势。
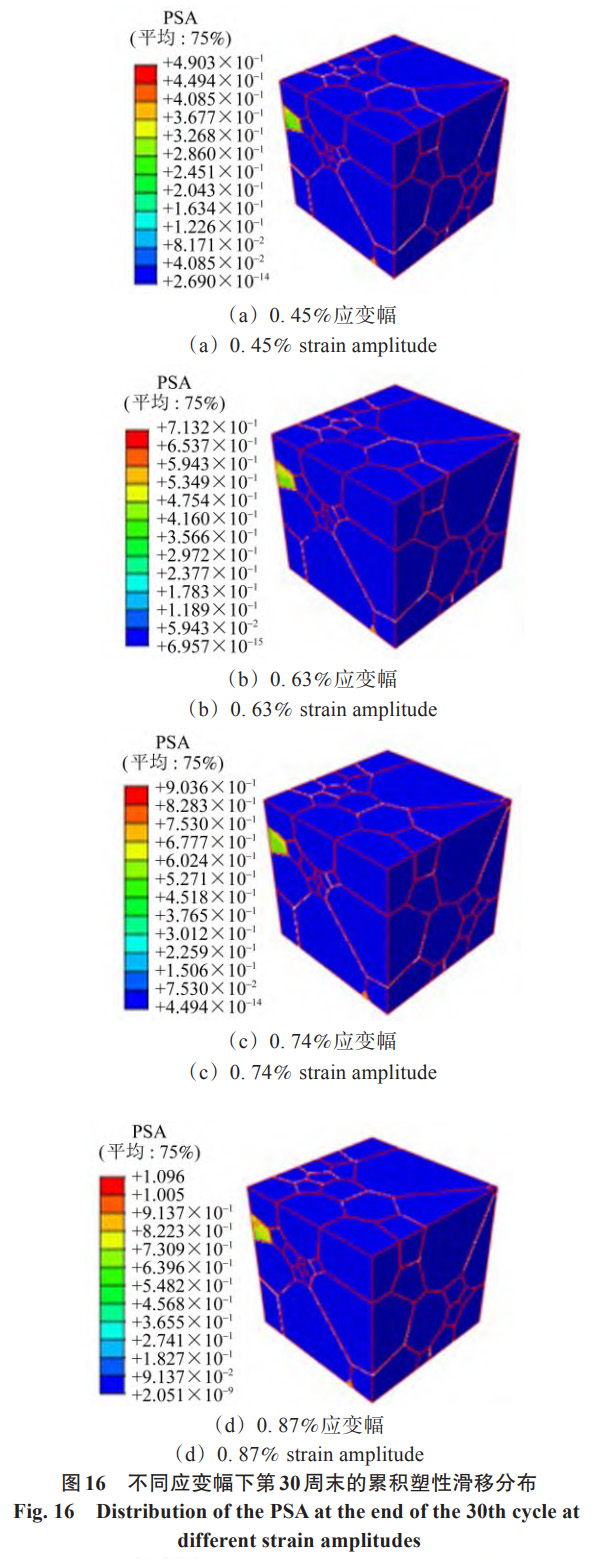
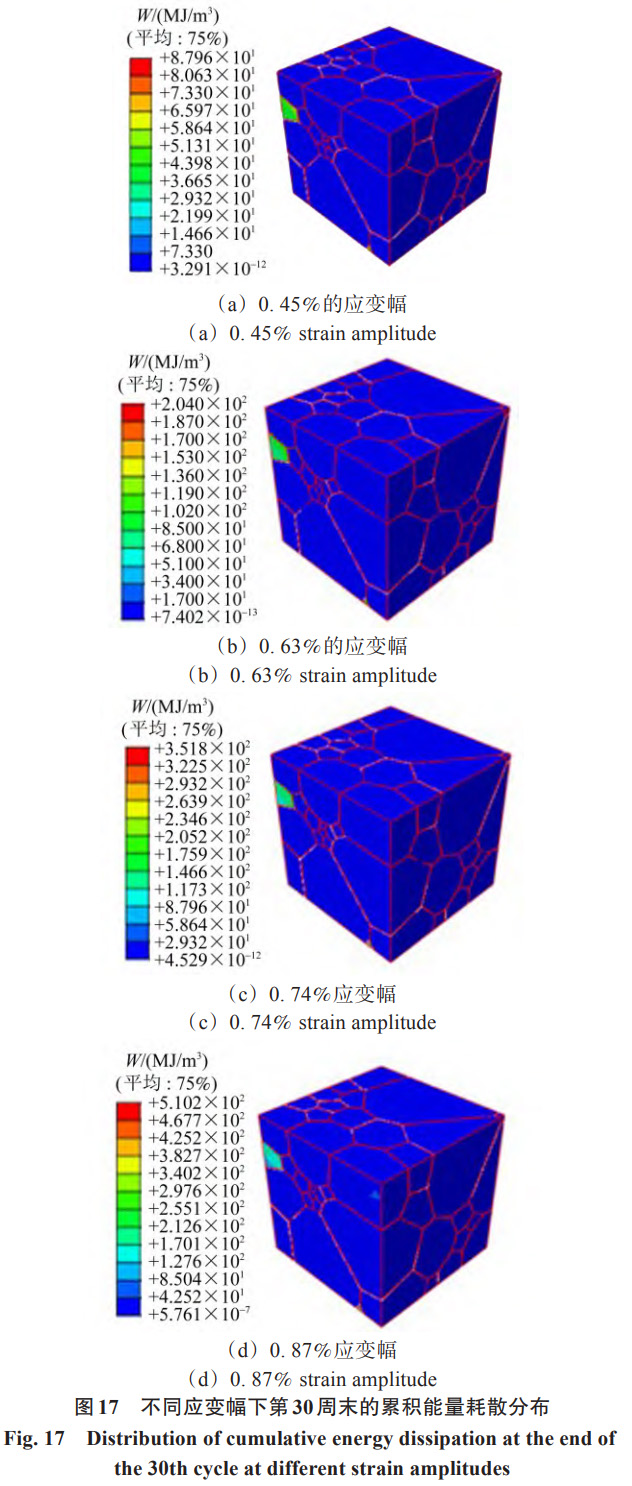
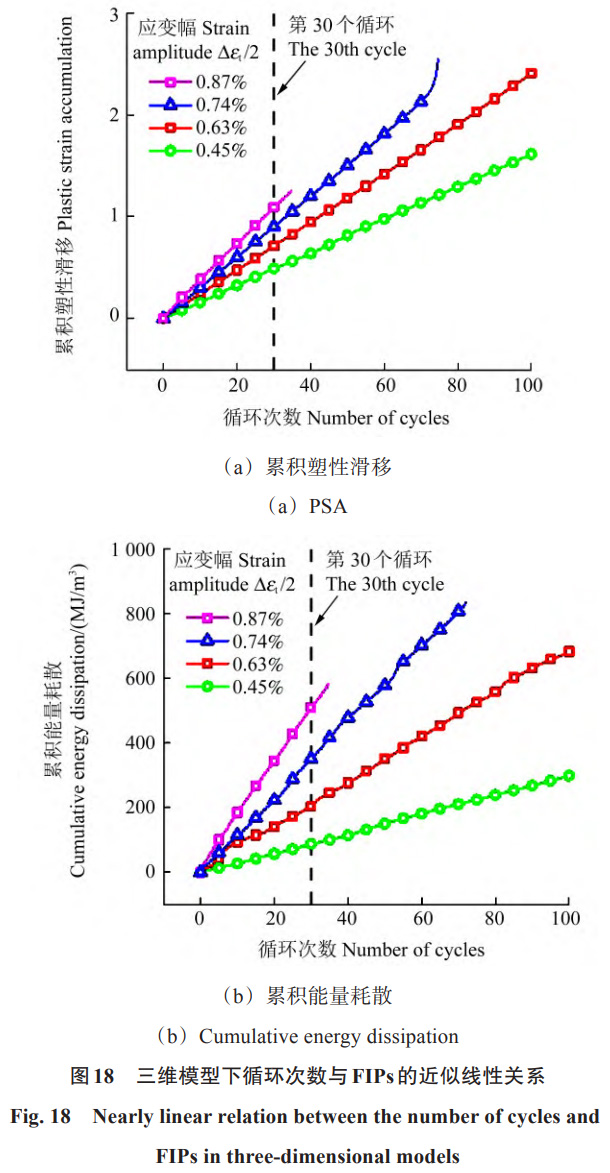
图 18 (a) 和图 18 (b) 为不同应变幅下 2 种疲劳指示因子随循环次数变化的规律。由图 18 可知,在三维结构中,循环次数与疲劳指示因子同样呈近似线性的关系。在应变幅为 0.63% 的条件下,借助试验所得的寿命数据和模拟至第 30 周末时的累积塑性滑移增量及累积能量耗散增量,利用式 (11) 和式 (13) 分别计算出,累积塑性滑移的临界值为 143,累积能量耗散的临界值为 30136 MJ/m³。为了进一步验证这些疲劳指示因子的有效性,图 19 对比了基于这 2 个因子预测的裂纹萌生寿命、采用疲劳安全寿命计算方法得出的预测寿命,以及实际的试验结果。由图 19 可知,基于疲劳指示因子的预测结果与试验结果高度吻合,且预测值相对保守;在预测准确性方面,基于疲劳指示因子的方法优于疲劳安全寿命计算方法。这一发现验证了累积塑性滑移和累积能量耗散作为疲劳指示因子在三维结构分析中的适用性。

4.4 讨论
尽管本研究在预测Ti6Al4V ELI钛合金的疲劳裂纹萌生寿命方面取得了初步成果,但仍存在诸多值得深入探讨和改进的问题,特别是在模型的维度、疲劳指示因子的线性假设以及试验观察方法上。本研究主要基于 EBSD 构建了Ti6Al4V ELI钛合金的疲劳裂纹萌生寿命预测模型,但这些模型主要局限于二维和简化的三维问题。尽管二维模型在计算效率和模型复杂性方面具有明显优势,但它无法全面考虑三维微观结构对疲劳行为的影响。实际上,材料的疲劳行为是一个复杂的三维问题,涉及晶粒的空间分布、相界面等多种因素。因此,未来的研究应致力于开发真实微观结构的三维模型,以更精确地模拟实际条件下的疲劳过程。在构建这些三维模型时,如何在计算复杂性和物理真实性之间找到平衡将是一个重大挑战。对于高度复杂的微观结构,可能需要借助先进的数值算法和高性能的服务器进行计算,以更准确地捕捉各个晶粒和相界面之间的相互作用。此外,本研究假设累积塑性滑移和累积能量耗散这 2 种疲劳指示因子与循环次数存在近似线性关系。然而,这 2 种疲劳指示因子在高疲劳加载条件下可能表现出非线性特性,因而上述线性假设虽然简化了模型,但可能导致对疲劳行为的预测不够精确。因此,未来的研究应考虑引入非线性疲劳指示因子,以更准确地描述材料在疲劳载荷下的真实响应。尽管本研究得出的结果与试验结果之间表现出良好的吻合性,为模型的有效性提供了有力支持,但将裂纹长度在 0~0.3 mm 假设为试验寿命对应的裂纹萌生寿命可能存在一定的局限性。为了更真实地反映裂纹萌生寿命,后续研究需要采用更先进的技术,如高分辨率成像技术或实时监测技术,来观察裂纹的萌生过程并测量所需数据。这些技术将有助于验证模型的预测能力并优化模型,从而提高疲劳寿命预测的准确性和可靠性。
5、结论
本研究致力于开发一个针对双相微观结构Ti6Al4V ELI钛合金的晶体塑性模型,以深入探究该材料的低周疲劳行为,并精确预测其裂纹萌生寿命。得出如下主要结论:
为双相Ti6Al4V ELI钛合金构建了一个基于真实微观结构的循环 CP 本构模型。此模型不仅考虑了背应力、分解切应力和滑移阻力的动态演变,还结合试验数据确定了相关的 CP 参数。此外,采用 2 种疲劳指示因子 (累积塑性滑移和累积能量耗散),以准确表征疲劳损伤程度。
研究显示,疲劳损伤更易在 α 相与 β 相的界面处萌生,这一现象与相邻晶粒间滑移阻力的差异密切相关。局部晶格旋转不仅加速了微观纹理的形成,还导致了累积塑性滑移和累积能量耗散的局部集中,从而加速了疲劳裂纹的产生。值得注意的是,每个循环中晶格旋转的不对称性引发了流动行为中拉伸与压缩的不对称性。
随着应变幅的增大,累积能量耗散和累积塑性滑移均呈显著上升趋势,而疲劳裂纹萌生寿命则相应缩短。通过与试验结果的对比发现,基于累积塑性滑移的疲劳指示因子相较于基于累积能量耗散的疲劳指示因子具有更高的预测准确性。与经典的 C-M 模型相比,基于疲劳指示因子的预测结果更清晰地展示了Ti6Al4V ELI钛合金因微观结构差异而导致的裂纹萌生寿命的显著差异。此外,这 2 种疲劳指示因子在三维结构中的适用性也得到了验证,其预测结果不仅准确,而且偏于保守,为工程应用提供了可靠的安全裕量。
参考文献 (References)
[1] CARRION P E, SHAMSAEI N, DANIEWICZ S R, et al. Fatigue behavior of Ti-6Al-4V ELI including mean stress effects [J]. International Journal of Fatigue, 2017, 99: 87-100.
[2] WANG F, CUI W C, PAN B B, et al. Normalised fatigue and fracture properties of candidate titanium alloys used in the pressure hull of deep manned submersibles [J]. Ships and Offshore Structures, 2014, 9 (3): 297-310.
[3] LIU C H, XU X, SUN T Z, et al. Microstructural effects on fatigue crack initiation mechanisms in a near-alpha titanium alloy [J]. Acta Materialia, 2023, 253: 118957.
[4] 高焱,金海波,李远杰,等。基于 FKM 的增材制造钛合金结构疲劳寿命分析方法研究 [J]. 机械强度,2024, 46 (4): 984-991. GAO Yan, JIN Haibo, LI Yuanjie, et al. Research on fatigue life analysis method of additive manufacturing titanium alloy structure based on FKM standard [J]. Journal of Mechanical Strength, 2024, 46 (4): 984-991. (In Chinese)
[5] LIN C W, JU C P, LIN J C. A comparison of the fatigue behavior of cast Ti-7.5Mo with c. p. titanium, Ti-6Al-4V and Ti-13Nb-13Zr alloys [J]. Biomaterials, 2005, 26 (16): 2899-2907.
[6] 吴连生,于培师,韦朋余,等。基于三维理论的 TC4ELI 钛合金疲劳裂纹扩展研究 [J]. 船舶力学,2022, 26 (9): 1354-1362. WU Liansheng, YU Peishi, WEI Pengyu, et al. Fatigue crack growth of TC4ELI titanium alloy based on three-dimensional theory [J]. Journal of Ship Mechanics, 2022, 26 (9): 1354-1362. (In Chinese)
[7] ZHAO Y X, YU P S, WU L S, et al. Corrosion-induced deceleration-to-acceleration of fatigue crack growth for deep-seaTi6Al4V ELItitanium alloy [J]. Engineering Fracture Mechanics, 2023, 281: 109160.
[8] BIAN J K, YU P S, ZHAO Y X, et al. Fatigue crack growth of marine 980 high-strength steel: from standard specimen testing to three-dimensional curved crack life prediction [J]. Ocean Engineering, 2024, 296: 116950.
[9] YU P S, GUO W L. An equivalent thickness conception for prediction of surface fatigue crack growth life and shape evolution [J]. Engineering Fracture Mechanics, 2012, 93: 65-74.
[10] YU P S, GUO W L. An equivalent thickness conception for evaluation of corner and surface fatigue crack closure [J]. Engineering Fracture Mechanics, 2013, 99: 202-213.
[11] 陶蒙,于培师,赵军华。基于晶体塑性与内聚力模型的 Cu-Ni-Si 合金晶界起裂研究 [J]. 机械强度,2024, 46 (5): 1184-1191. TAO Meng, YU Peishi, ZHAO Junhua. Study on crack initiation at grain boundary of Cu-Ni-Si alloy based on crystal plasticity and cohesive zone model [J]. Journal of Mechanical Strength, 2024, 46 (5): 1184-1191. (In Chinese)
[12] 张海英,李刚,臧伟锋,等。激光选区熔化 Ti-6Al-4V 钛合金疲劳裂纹扩展性能研究 [J]. 机械强度,2023, 45 (6): 1355-1360. ZHANG Haiying, LI Gang, ZANG Weifeng, et al. Fatigue crack growth performance of Ti-6Al-4V titanium alloy by selective laser melting [J]. Journal of Mechanical Strength, 2023, 45 (6): 1355-1360. (In Chinese)
[13] WANG L, YE C, SUN C Q, et al. Experimental investigation on compressive dwell fatigue behavior of titanium alloy pressure hull for deep-sea manned submersibles [J]. Ocean Engineering, 2024, 303: 117646.
[14] CHAN K S. Roles of microstructure in fatigue crack initiation [J]. International Journal of Fatigue, 2010, 32 (9): 1428-1447.
[15] LU X C, ZHAO J F, YU C, et al. Cyclic plasticity of an interstitial high-entropy alloy: experiments, crystal plasticity modeling, and simulations [J]. Journal of the Mechanics and Physics of Solids, 2020, 142: 103971.
[16] MANONUKUL A, DUNNE F P E. High- and low-cycle fatigue crack initiation using polycrystal plasticity [J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2004, 460 (2047): 1881-1903.
[17] KORSUNSKY A M, DINI D, DUNNE F P E, et al. Comparative assessment of dissipated energy and other fatigue criteria [J]. International Journal of Fatigue, 2007, 29 (9/10/11): 1990-1995.
[18] ZHANG K S, JU J W, LI Z H, et al. Micromechanics based fatigue life prediction of a polycrystalline metal applying crystal plasticity [J]. Mechanics of Materials, 2015, 85: 16-37.
[19] SANGID M D, MAIER H J, SEHITOGLU H. A physically based fatigue model for prediction of crack initiation from persistent slip bands in polycrystals [J]. Acta Materialia, 2011, 59 (1): 328-341.
[20] YUAN G J, ZHANG X C, CHEN B, et al. Low-cycle fatigue life prediction of a polycrystalline nickel-base superalloy using crystal plasticity modelling approach [J]. Journal of Materials Science & Technology, 2020, 38: 28-38.
[21] SWEENEY C A, O’BRIEN B, DUNNE F P E, et al. Strain-gradient modelling of grain size effects on fatigue of CoCr alloy [J]. Acta Materialia, 2014, 78: 341-353.
[22] YUAN G J, WANG R Z, GONG C Y, et al. Investigations of micronotch effect on small fatigue crack initiation behaviour in nickel-based alloy GH4169: experiments and simulations [J]. International Journal of Fatigue, 2020, 136: 105578.
[23] YUAN G J, WANG R Z, ZHU W B, et al. Experimental and simulated investigations of low cycle fatigue behavior in a nickel-based superalloy with different volume fractions of δ phase [J]. International Journal of Fatigue, 2021, 153: 106411.
[24] CRUZADO A, LUCARINI S, LLORCA J, et al. Microstructure-based fatigue life model of metallic alloys with bilinear Coffin-Manson behavior [J]. International Journal of Fatigue, 2018, 107: 40-48.
[25] MCDOWELL D L, DUNNE F P E. Microstructure-sensitive computational modeling of fatigue crack formation [J]. International Journal of Fatigue, 2010, 32 (9): 1521-1542.
[26] PRZYBYLA C P, MUSINSKI W D, CASTELLUCCIO G M, et al. Microstructure-sensitive HCF and VHCF simulations [J]. International Journal of Fatigue, 2013, 57: 9-27.
[27] MCDOWELL D L. Simulation-based strategies for microstructure-sensitive fatigue modeling [J]. Materials Science and Engineering: A, 2007, 468: 4-14.
[28] LIU W C, HUANG J, LIU J W, et al. Experimental and crystal plasticity modelling study on the crack initiation in micro-texture regions of Ti-6Al-4V during high cycle fatigue tests [J]. International Journal of Fatigue, 2021, 148: 106203.
[29] 全国钢标准化技术委员会。金属材料 拉伸试验 第 1 部分:室温试验方法:GB/T 228.1-2021 [S]. 北京:中国标准出版社,2021: 12-15. National Technical Committee of Steel Standardization. Metallic materials: tensile testing: part 1: method of test at room temperature: GB/T 228.1-2021 [S]. Beijing: Standards Press of China, 2021: 12-15. (In Chinese)
[30] LIU L Y, YANG Q S, LIU X, et al. Crystal cracking of grain-gradient aluminum by a combined CPFEM-CZM method [J]. Engineering Fracture Mechanics, 2021, 242: 107507.
[31] MATSUMOTO H, YOSHIDA S, SASE R, et al. Crystallographic rotation of Ti-6Al-4V alloy with a fiber texture component under isothermal forging through experimental and CPFEM analyses [J]. Materialia, 2023, 30: 101839.
[32] ZHOU D W, WANG X W, YANG X Y, et al. A generalized physical-based failure indicator parameter used in crystal plasticity model to predict fatigue life under low cycle fatigue and creep-fatigue loadings [J]. International Journal of Fatigue, 2023, 166: 107290.
[33] BALASUBRAMANIAN S, ANAND L. Plasticity of initially textured hexagonal polycrystals at high homologous temperatures: application to titanium [J]. Acta Materialia, 2002, 50 (1): 133-148.
[34] OGI H, KAI S, LEDBETTER H, et al. Titanium’s high-temperature elastic constants through the hcp-bcc phase transformation [J]. Acta Materialia, 2004, 52 (7): 2075-2080.
[35] HE T, TANG Y X, WU H B, et al. Research and analysis of TC4 titanium alloy cutting based on crystal plasticity theory [J]. Journal of Physics: Conference Series, 2024, 2785 (1): 012131.
[36] ZHANG K, WU X, DAVIES C H J. Effect of microtexture on short crack propagation in two-phase titanium alloys [J]. International Journal of Fatigue, 2017, 104: 206-220.
[37] 王雷,王琨,李艳青,等. TC4ELI 钛合金低周疲劳性能研究 [J]. 钛工业进展,2018, 35 (2): 17-21. WANG Lei, WANG Kun, LI Yanqing, et al. Low-cycle fatigue properties of TC4ELI titanium alloy [J]. Titanium Industry Progress, 2018, 35 (2): 17-21. (In Chinese)
(注,原文标题:基于微结构特征的Ti6Al4V_ELI钛合金疲劳裂纹萌生寿命晶体塑性预测方法)
tag标签:Ti6Al4V,ELI钛合金,深海服役,疲劳安全性评估



